Weighting

A toolkit for calculating weights in IceCube simulation

Introduction

Experimental data from an instrument like IceCube are ultimately just a set of counts. These are typically expressed as rates, which are independent of the observation time:

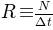
In order to simulated data to real data, it is necessary to calculate the rate predicted by the simulation. Most simulation in IceCube is weighted, meaning that it is generated from a spectrum that does not necessarily reflect any realistic physical model, and you must calculate weights that reflect the frequency of any given event in the model of interest. These models are given as differential fluxes:

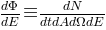
that is, a number of expected events per unit time, area, solid angle, and energy. The generation spectrum of the simulation is a differential fluence, that is, the total number of events generated per unit area, solid angle, and energy. The ratio of the two is a weight in units of :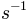

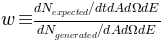
While simple in principle, the calculation of the weight given above can be quite tedious, especially when multiple particle types or overlapping energy ranges are involved. This project automates the calculation of the denominator in the above equation for the most common types of simulation used in IceCube, and also provides implementations of a few flux models that can be used in the numerator to weight cosmic ray simulations.

Tutorial

For the following examples, we will assume that we are working from an HDF5 file produced by tableio, with a table named “MCPrimary” containing the generated cosmic ray::

>>> import tables
>>> hdf = tables.openFile('corsika.hdf5')
>>> hdf.root
/ (RootGroup) ''
  children := ['CorsikaWeightMap' (Table), '__I3Index__' (Group), 'MCPrimary' (Table)]

Getting normalizations for SimProd datasets

In the most common use case, you just want to calculated weights for an official simulation set. Luckily the generator settings are stored in the Simulation Production database, and we can construct the normalization term automatically from the dataset number::

>>> from icecube.weighting import weighting
>>> nfiles, generator = weighting.from_simprod(10087)
>>> generator *= nfiles

By default nfiles gives the total number of files in the dataset. If have only a subset of the files, you should use that number instead.

Weighting “unweighted” dCORSIKA to a different flux model

While we have a lot of simulation lying around generated with the Hoerandel model, it does not describe our data terribly well. Luckily, though, it can be re-weighted to reflect a different flux model::

>>> from icecube.weighting.fluxes import GaisserH3a
>>> from icecube.weighting.weighting import Hoerandel, I3Units
>>> generator = Hoerandel(nevents=25e7, emin=6e2*I3Units.GeV, emax=1e11*I3Units.GeV)
>>> flux = GaisserH3a()
>>> energy = hdf.root.MCPrimary.cols.energy[:]
>>> ptype = hdf.root.MCPrimary.cols.type[:]
>>> weights = flux(energy, ptype)/generator(energy, ptype)
>>> weights
array([ 0.11307773,  0.16582993,  0.11443925, ...,  0.10568692,
        0.12293974,  0.10502099])
>>> weights/(1./hdf.root.CorsikaWeightMap.cols.TimeScale[:])
array([ 1.13484598,  1.66426601,  1.1485101 , ...,  1.06067193,
        1.23382088,  1.05398866])

Weights for combined dCORSIKA sets with overlapping energy ranges

If energy ranges for two simulation sets overlap, then the weights must be adjusted to account for the fact that more events are generated in the overlap region of the combined sample than in either one individually. In this example, we’ll use the from_simprod() convenience method to look up the dCORSIKA configuration in the Simulation Production database. 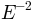In this case, we’ll combine a set generated on an spectrum with one generated on an 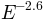spectrum::

>>> from icecube.weighting.weighting import from_simprod
>>> hard = from_simprod(6514)[1]
>>> soft = from_simprod(9654)[1]

If we have 100k files from the hard spectrum and 77k from the soft spectrum, the normalization is the sum of the individual generators::

>>> generator = 1e5*hard + 77e4*soft

After that, the procedure is exactly the same as for the single-set case::

>>> hdf = tables.openFile('combined_corsika.hdf5')
>>> energy = hdf.root.MCPrimary.cols.energy[:]
>>> ptype = hdf.root.MCPrimary.cols.type[:]
>>> weights = flux(energy, ptype)/generator(energy, ptype)

Weighting NeutrinoGenerator simulation to an atmospheric flux

For NeutrinoGenerator simulation, the weight map has a different name and different contents::

>>> hdf = tables.openFile('nugen.hdf5')
>>> hdf.root
/ (RootGroup) ''
  children := ['I3MCWeightDict' (Table), '__I3Index__' (Group), 'MCPrimary' (Table)]

Note

This example uses atmospheric flux models implemented in the NewNuFlux project.

Weighting NeutrinoGenerator simulation requires a few extra complications. Since interactions are forced, the interaction probability needs to be multiplied into the weight. Also, atmospheric neutrino fluxes depends on zenith angle, and are given in different units::

>>> from icecube import NewNuFlux
>>> from icecube.icetray import I3Units
>>> flux = NewNuFlux.makeFlux('honda2006').getFlux
>>> generator = from_simprod(9250)[1]
>>> energy = hdf.root.MCPrimary.cols.energy[:]
>>> ptype = hdf.root.MCPrimary.cols.type[:]
>>> cos_theta = numpy.cos(hdf.root.MCPrimary.cols.zenith[:])
>>> p_int = hdf.root.I3MCWeightDict.cols.TotalInteractionProbabilityWeight[:]
>>> unit = I3Units.cm2/I3Units.m2
>>> weights = p_int*(flux(ptype, energy, cos_theta)/unit)/generator(energy, ptype)

NeutrinoGenerator calculates and stores a quantity called “OneWeight” that is analogous to the inverse of the generated fluence. In this case we can use it to double-check our calculation::

>>> oneweight = flux(ptype, energy, cos_theta)*hdf.root.I3MCWeightDict.cols.OneWeight[:]/(hdf.root.I3MCWeightDict.cols.NEvents[:]/2)
>>> weight/oneweight
array([ 1.,  1.,  1., ...,  1.,  1.,  1.])

In the above calculation we had to divide by 2 to account for the fact that NeutrinoGenerator generates equal numbers of neutrinos and anti-neutrinos of the configured flavor.

Calculating an effective area with NeutrinoGenerator

TODO

Event generator details

Some details of how each event generator works are necessary in order to fully understand the weighting scheme.

dCORSIKA

dCORSIKA (our private branch of the CORSIKA air shower simulation package) can be run in one of two modes. In the “unweighted” mode, it generates primary cosmic rays from proton through iron proportional to the spectrum from the Hoerandel paper (power laws with rigidity-dependent knees). In the “five-component” mode, it generates proton, He, N, Al, and Fe nuclei on unbroken power laws, with separately configurable power law indices and relative normalizations for each component. In both modes the lower bound of the energy range is often in energy per nucleon rather than energy per nucleus, e.g. for a lower bound of 1 TeV, the lowest-energy Fe nucleus would have an energy of 56 TeV.

The target surface for dCORSIKA simulation is an upright cylinder centered on the origin of the IceCube coordinate system, and typically extending several hundred meters beyond the edge of the instrumented volume. Each shower is simulated with an axis that passes through a fixed point; when the files are read in to IceTray the shower axes are distributed uniformly in the area of the target cylinder projected along the shower direction. The distribution of generated zenith angles is biased so that it is proportional to the projected area of the target cylinder, so the effective fluence of shower axes through the surface is isotropic.

Target surface used in dCORSIKA.

NeutrinoGenerator

NeutrinoGenerator generates an equal number of neutrinos and anti-neutrinos of a given flavor on an unbroken power law, propagates them through the Earth, and forces them to interact in the final simulation volume. The probability of the interaction actually occuring is a function of the interaction cross-section and is recorded for later use as a weight. The sampling surface is a disc perpendicular to the neutrino direction and centered on the origin of the coordinate system; the neutrino axes are distributed uniformly over this area.

Target surface used in NeutrinoGenerator

API

class icecube.weighting.weighting.GenerationProbability(emin, emax, nevents=1, area=1, particle_type=None)

A probability distribution from which MC events are drawn.

Generation probabilities may be multiplied by an integer to express a joint generation probability for multiple identical simulation runs or added together to express a set of distinct runs.

icecube.weighting.weighting.FiveComponent(nevents, emin, emax, normalization=[10.0, 5.0, 3.0, 2.0, 1.0], gamma=[-2.0, -2.0, -2.0, -2.0, -2.0], spric=True, height=1600, radius=800)

Special case: 5-component dCORSIKA

Parameters:

• normalization – relative normalizations of the 5 components
• gamma – power law index for each component
• spric – make lower energy proportional to primary mass
• height – full height of the target cylinder in meters
• radius – radius of the target cylinder in meters

Note

The return value of the GenerationProbability will be in units of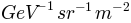

icecube.weighting.weighting.Hoerandel(nevents, emin, emax, dslope=0, height=1600, radius=800)

Special case: in RANPRI=2 mode, dCORSIKA produces a “natural” spectrum after the parameterization of Hoerandel. In order to combine this with 5-component simulation we use only H, He, N, Al, and Fe, ignoring all other components.

Parameters:

• dslope – multiply all fluxes by E^dslope
• height – full height of the target cylinder in meters
• radius – radius of the target cylinder in meters

Note

The return value of the GenerationProbability will be in units of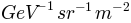

icecube.weighting.weighting.NeutrinoGenerator(NEvents, EnergyMinLog, EnergyMaxLog, GammaIndex, NeutrinoFlavor, InjectionRadius=1200.0, ZenithMin=0, ZenithMax=3.141592653589793, AzimuthMin=0, AzimuthMax=6.283185307179586, **kwargs)

Construct a GenerationProbability appropriate for NeutrinoGenerator simulation. The arguments have the same meaning as those to the I3NeutrinoGenerator.

Warning

The return value of the GenerationProbability will be in units of 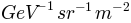rather than 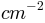. Make sure that you use fluxes in the appropriate units!

icecube.weighting.weighting.from_simprod(dataset_id, use_muongun=False)

Extreme laziness: parse weighting scheme out of the simulation production database

Parameters:dataset_id – the number of the SimProd dataset Returns:a tuple whose first element is the number of files that finished processing successfully, and the second