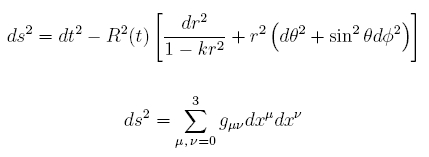
2. ELECTROMAGNETIC OBSERVATIONS

2.4    MULTI-WAVELENGTH AFTERGLOWS

2.4.2    SPECTROSCOPIC REDSHIFT

    The cosmological principle postulates a homogenous and isotropic universe. Due to its maximal spatial symmetry, the invariant Friedmann-Robertson-Walker (FRW) line element (ds²) provides a kinematical framework since it selects a unique metric tensor (g_mn) consistent with the cosmological principle and observation (Spergel et al. 2003, Tegmark et al. 2004 & Pope et al. 2004) by separating r and t, such that:

    Since R is a function of time, it provides a scale factor for distances in comoving coordinates (r, q, f). Spatial curvature is described by the value of k, such that values of -1, 0, +1 correspond to open, flat and closed spatial geometries, respectively, as illustrated in figure 2.4.2.1.

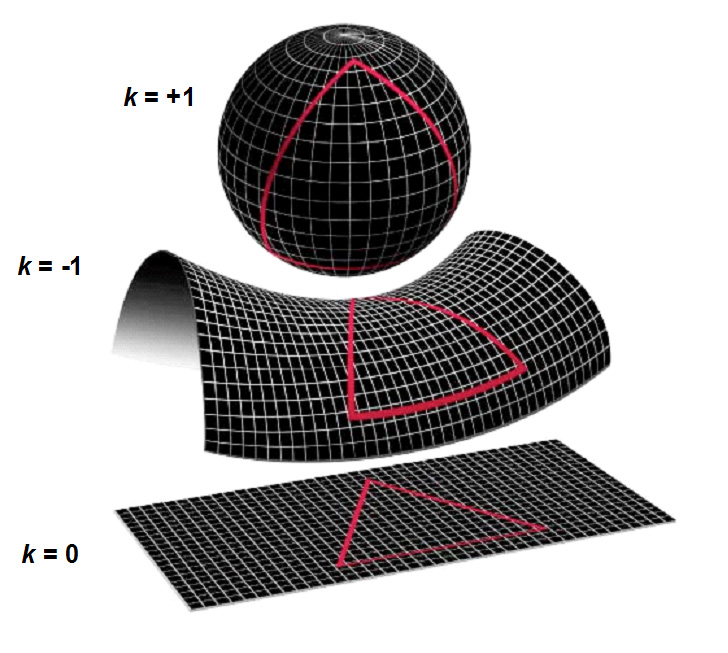
FIGURE 2.4.2.1: Schematic representation of spatial geometries.

    A dynamical description of the expansion of the universe requires solutions to the equations of motions defined by the general theory of relativity, known as the Einstein field equation,

Where G_mn and T_mn are known as the Einstein and stress-energy tensors respectively, while L is known as the cosmological constant. The FRW metric yields two independent solution known as the Friedmann-Lemaître equations (Pal 1999)

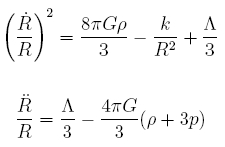
Where r is density and p is pressure. The Hubble parameter (H), defines the expansion rate which can be expressed as

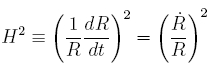
For present day values,

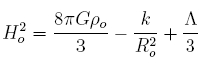
where r_o describes the total energy density, comprised of matter and radiation. Typically, the cosmological parameters are cast in terms of the following density fractions:

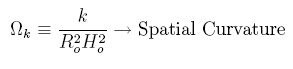
which are normalized as follows:

The comoving (transverse) radial proper distance is then defined as:

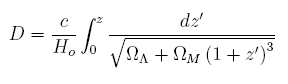
Here we introduce the redshift parameter, z, such that:

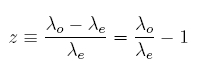
where l_e and l_o are the emitted and observed wavelengths, respectively. Hubble expansion increases the photon wavelength and decreases the frequency which each decrease the photon energy by a factor of 1+z. The luminosity distance (d_L), is defined as the distance to the source if the fluence, flux or apparent brightness obeyed a simple inverse square law, assuming  isotropic emission, as illustrated in figure 2.4.2.2., such that:

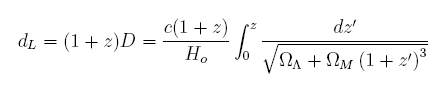
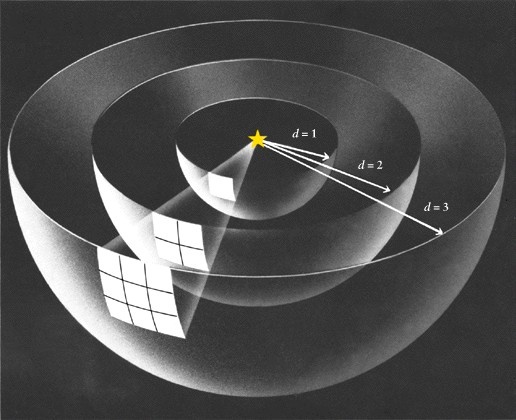
FIGURE 2.4.2.2: Schematic of spherically isotropic electromagnetic emission for various luminosity distances (d=1, 2 & 3). The luminosity distance is defined such that the apparent brightness of the source follows an inverse square law, e.g. F_g ~ d_L^-2.

    Spectroscopic redshifts, via direct doppler measurement of GRB afterglow emissions or their host galaxies (Kulkarni et al. 2000, Djorgovsk et al. 2001), have placed long duration GRBs at cosmological distances with redshifts spanning 0.0085 ≤   z ≤ 4.511, as illustrated in figure 2.4.2.3. Furthermore, it has been argued (Lamb & Reichart 2000) that GRBs are expected to occur at z ~ 10 and possibly to z ~ 15-20. This has been corroborated by empirical redshift estimation methods based upon prompt g-ray emission observables from BATSE GRBs (Fenimore & Ramirez-Ruiz 2000, Band et al. 2004, Yonetoku et al. 2004).

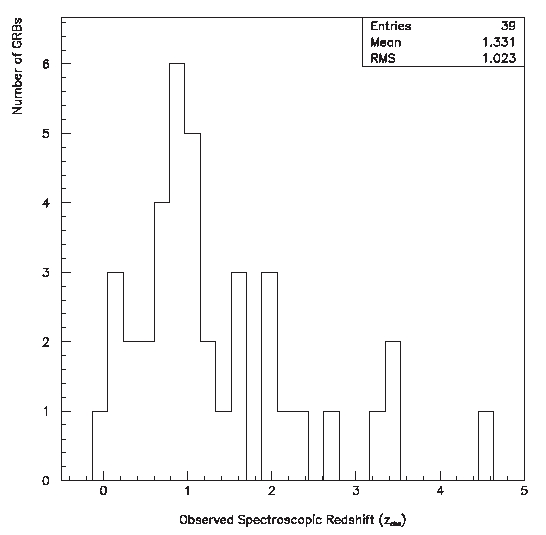
FIGURE 2.4.2.3: Distribution of spectroscopic redshifts for GRBs.

    The observed spectroscopic redshift of the OT associated with GRB030329, acquired using the Low Resolution Imaging Spectrometer (LRIS 2001) on the Keck I telescope (Keck 2005), is illustrated in figure 2.4.2.4. Image Reduction and Facility software (IRAF 2005) was used to reduce and extract the spectrum, which was accumulated over a 600^s exposure time with an effective resolution of 4.2 Angstrom. Absorption lines from Mg II (due to gas within the galactic disk) and emission lines from O II, Hb and O III (typical for star-forming regions) were observed at mean redshift of z = 0.169 +/- 0.001 (Price et al. 2003), which was confirmed by independent measurements of z = 0.1685 (Greiner et al. 2003) and z = 0.168 (Caldwell et al. 2003). The feature from Ca II, at z = 0, is assumed to be an artifact of our own Milky Way galaxy.

FIGURE 2.4.2.4: The observed OT spectrum (Price et al. 2003) from the Low Resolution Imaging Spectrometer (LRIS 2001)  on the Keck I telescope (Keck 2005).

    It should be noted that although a redshift of 0.169 ± 0.001 is relatively close, with respect to canonical GRB distances (z ~ 1), it is still cosmological in nature. Under a L_CDM cosmology  (Spergel et al. 2003, Tegmark et al. 2004 & Pope et al. 2004)  with: H = (72 +/- 5) km/(Mpc s), W_M = 0.29 +/- 0.07  and W_L = 0.73 +/- 0.07, a redshift of 0.169 corresponds to a comoving radial distance of 678⁺⁶¹_-53 Mpc, which translates into ~2.2 billion light years. To put this in perspective, consider that this event occurred during Precambrian time (Proterozoic eon, Paleoproterozoic era, Rhyacian period). At this time in Earth's geologic history, the first ice age had not occurred and the land mass that would later become Antarctica was actually located in the northern hemisphere!