Comparison between Single and
32-fold Iterative Likelihoods
Here we show some results comparing the Single and the 32-fold
Iterative Likelihood, in the context of the preparation of the steering
file for the 2005 data filtering at UW.
The sample used to produce these results consists of CORSIKA-generated down-going muons. The total number of events at the detector level is 56439.
The Sieglinde steering file used for the analysis of these events is here.
Therefore, the fake rate for the Iterative Likelihood is higher than for the Single Likelihood.
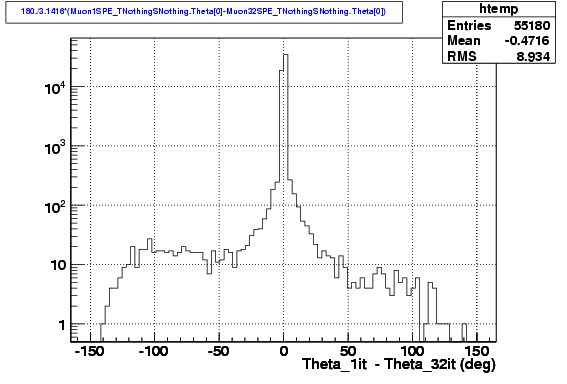
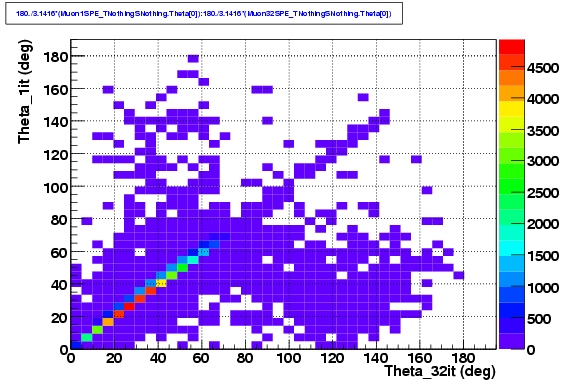
We can also plot the difference between the reconstructed zenith angle in both cases, and we see that there is ineed an asymmetry: in case of disagreement, the Iterative LH has a larger chance to produce a fake.
The sample used to produce these results consists of CORSIKA-generated down-going muons. The total number of events at the detector level is 56439.
The Sieglinde steering file used for the analysis of these events is here.
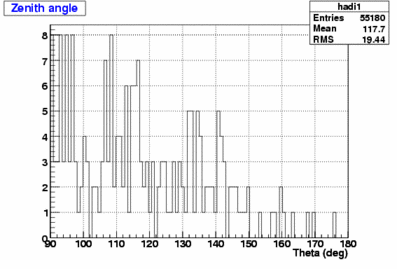 280 fake events (0.38%) |
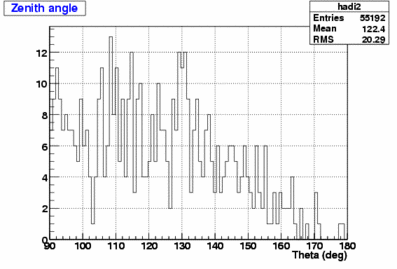 501 fake events (0.89%) |
Therefore, the fake rate for the Iterative Likelihood is higher than for the Single Likelihood.
We can also plot the difference between the reconstructed zenith angle in both cases, and we see that there is ineed an asymmetry: in case of disagreement, the Iterative LH has a larger chance to produce a fake.


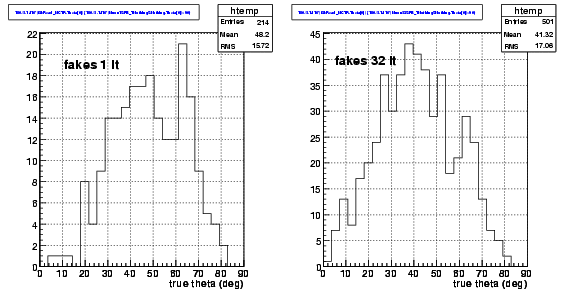
We compare now the
distributions of true zenith angle when a fake is produced. We see that
there are not large differences, although the mean true zenith angle of
fakes with SingleLH is larger than for Iterative LH:

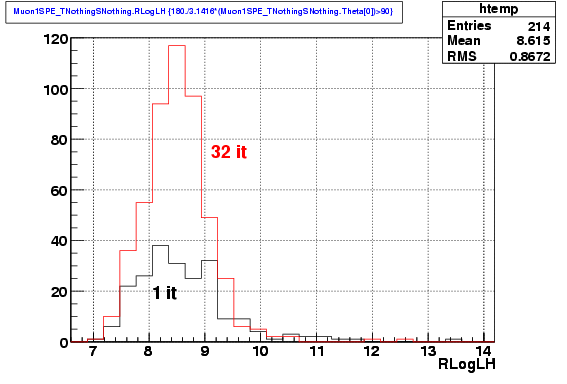
The distributions of the reduced likelihood does not present great differences in shape:

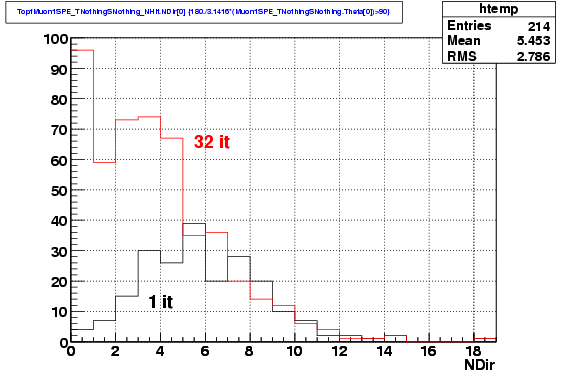
The
distributions of the number of direct hits, on the other hand, are
clearly different. For Iterative LH we see a large fraction of events
with low number of hits. This gives a hint that probably most of these
fake events are going to be rejected with the selection cuts.

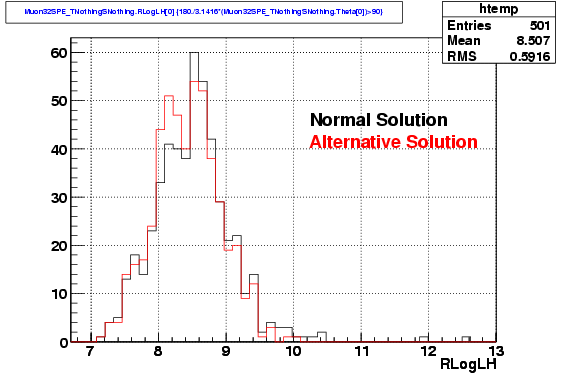
Here we compare
the distribution of reduced likelihood (for the 32-fold iterative
method) using the normal solution and the best solution in the other
hemisphere. As suspected, this indicates that the alternative solution
is has a value very close to the best solution.

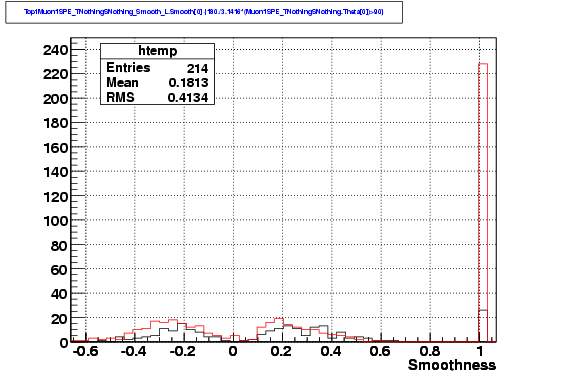
The
distribution of smoothness show clearly that many of the extra fake
events in the Iterative Likelihood do not have a physical value. These
events will be removed in any analysis, which makes the difference in
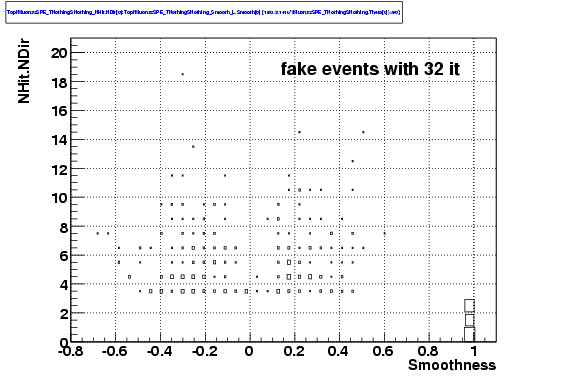
the fake rate much smaller. Those events, as shown in the last plot,
have a very small number of direct hits.

