Final cut selection
Distributing Events Among the Burst Sample

    In satellite-coincident AMANDA analyses, the way the total number of signal events are split between the observed bursts is unimportant, since it is really the total flux from all bursts observed that matters.  However, one has a better chance of observing a cluster of N events ocurring at the same time while looking at one burst that has an expectation of N events rather than ten weaker bursts each with expectation of N/10 events, even though the flux is the same.  Therefore, the way the flux is divided amongst bursts is important for the rolling search because it looks for a cluster of events in temporal coincidence.  Therefore, rather than assuming equal flux for each burst, I am using a more realistic distribution, which I will refer to as the "Guetta" distribution.  This assigns a different expected event rate to each burst, based on rates predicted for actual bursts as given in Guetta et al and plotted below.  In my Monte Carlo, each burst has an expected event rate which is the average rate multiplied by some factor.  This multiplicative factor is selected by randomly sampling from a distribution based on the Gaussian fit to the data in the plot below.  Most bursts will have an expected rate near the average rate, but some will be substantially brighter and some dimmer, as is really the case.

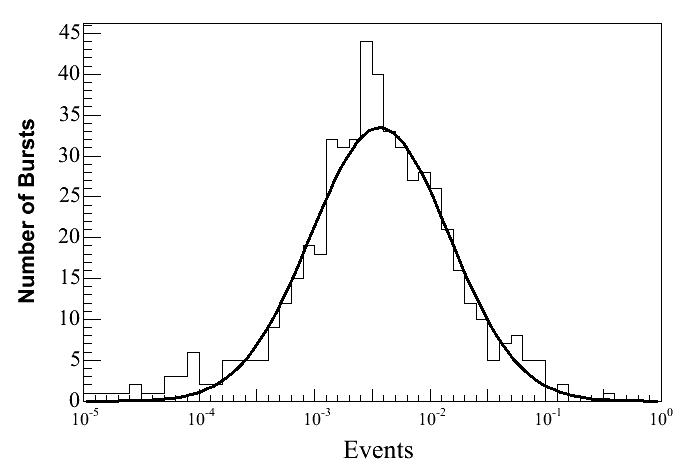
burstdists.gif

Distribution of expected events from actual BATSE bursts



Cut Selection Based on Model Discovery Potential

    Since the sensitivity of this analysis to conventional GRBs will be above that of previous AMANDA analyses, it was decided to optimize for discovery (although it turns out that the sensitivity we obtain at cuts based on discovery is not much different than what one obtains from the MRF).  In precise terms, optimizing for discovery in this case means finding the cuts such that we have a 90% of getting a signal with at least 5 sigma significance at the lowest possible flux.  Model Discovery Potential plots for both searches are shown below, with event distributions modeled by the afforementioned "Guetta" distribution.  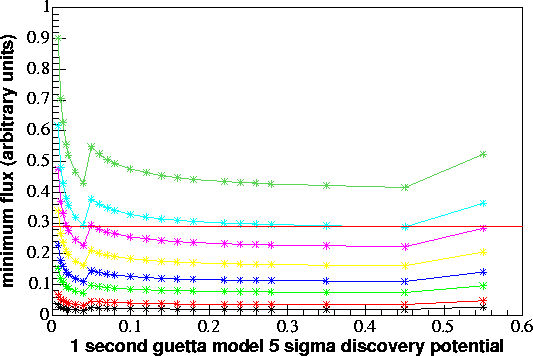The x-axis shows SVM cost factor (equivalent to tightness of cuts at the final level) with tighter cuts on the left of the plot and looser cuts on the right.  The y-axis shows the minimum flux (in average events per burst) one needs to have a certain percent chance to see a signal with at least 5 sigma significance.  For example, the light blue line shows the minimum signal flux one would need at each cost factor to have a 90% chance of seeing a 5 sigma signal.  While the 90% line was the one selected to base cuts on, one obtains very similar results foor anything above 25%.  The cuts selected based on these two plots are cost factor .08 (80.9% signal retention) for the 100 second search and .45 (96% signal retention) for the 1 second search, although these are very close to the minima at smaller cost factors, which would require fewer events for a 5 sigma detection, but also cut away a larger percentage of the signal.  (The horizontal red line is drawn on the 1 second plot to demonstrate that .45 really gives the minimum, albeit by a small margin.)

fmdf.5sig.guetta.100s.gif   mdf.5sig.guetta.1s.gif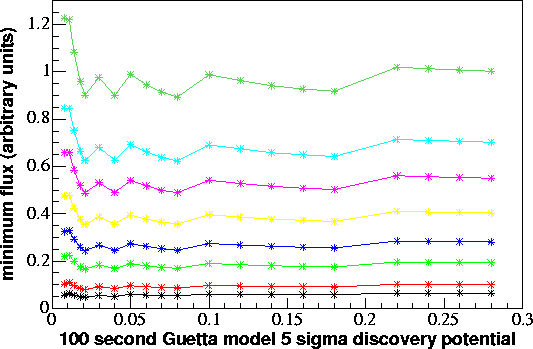

Statistical power:  dark green - 99%, light blue - 90%, violet - 75%, yellow - 50%, blue - 25%, light green - 10%, red - 1%, black - 0.1%



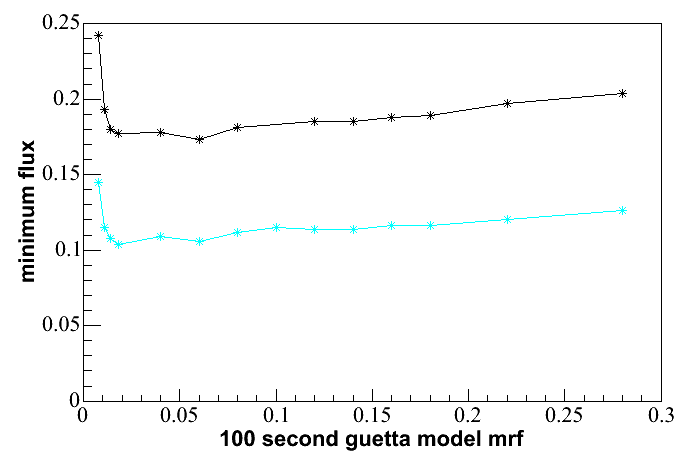
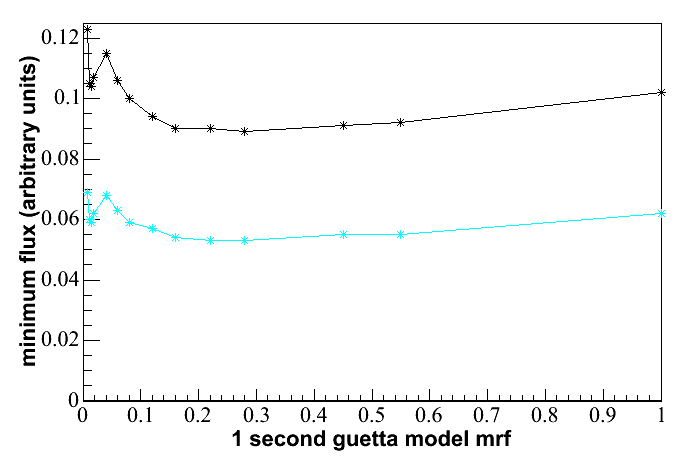
Model Rejection Potential

Model Rejection Potentail plots obtained using the "Guetta" distribution are shown below.  Again, cost factor (equivalent to tightness of cuts) is shown on the x-axis.  The mrf at the cut levels selected by the Model Discovery Potential method are only 7.7% above the minimum in the case of the 100 second search and 3.2% above the minimum in the case of the 1 second search, so in this case there turns out not to be much difference between optimizing for limit setting and optimizing for discovery.

mrf2.guetta.100s.gif


mrf2.guetta.1s.gif


Comparison With Other Ways of Distributing Events Among Bursts


    In addition to the "Guetta" distribution described above, I also looked at two more simplified distributions of events.  In the "single" burst distribution, all flux from the entire year is placed in a single burst, meant to simulate a case in which one burst dominates.  In the "flat" distribution, the flux is divided equally among all bursts.  This is unrealistic, but serves as a sort of "default" distribution that is useful for comparison.
    The following table summarizes the minima for the Model Rejection Potential as well as Model Discovery Potential at 3, 4 and 5 sigma for each of the three methods of distributing events between bursts.  In general, the "Guetta" distribution and "single" burst distribution have values where we are taking the cuts that are fairly close to optimal both in terms of sensitivity and discovery potential.  It is unsurprising that the "Guetta" and "single burst" distributions would yield similar results, since the "Guetta" model will be generally yield one to a few bursts per year which are dominant in terms of signal detection prospects.  The "flat" distribution (equal flux for each burst) would lead to cuts which are tighter than those we are taking, but this is a less realistic model.


 100 second search minimum
 % diff between minimum and selected cut
 1 second search minimum
 % diff between minimum and selected cut
Guetta Distribution



3 sigma
 0.08
 0%
 0.55
 1.1%
4 sigma
 0.04
 2.7%
 0.16
 28.6%
5 sigma
 0.08
 0%
 0.45
 0%
MRF
 0.018
 7.7%
 0.28
 3.8%





Single Burst



3 sigma
 0.08
 0%
 0.55
 0.7%
4 sigma
 0.08, 0.18
 0%
 0.16
 11.4%
5 sigma
 0.18
 1.3%
 0.45
 0%
MRF
 0.08
 0%
 0.35
 1.9%





Flat Distribution



3 sigma
 0.014
 29.5%
 0.04
 40.7%
4 sigma
 0.018
 23.1%
 0.014
 54.3%
5 sigma
 0.021
 16.2%
 0.04
 12.9%
MRF
 0.014
 30.0%
 0.014
 20.1%


Back