Unblinding Proposal for "Rolling" Cascade

GRB Search 2001

Results

The results of the analysis are consistent with background for both the 100 second and 1 second search windows.

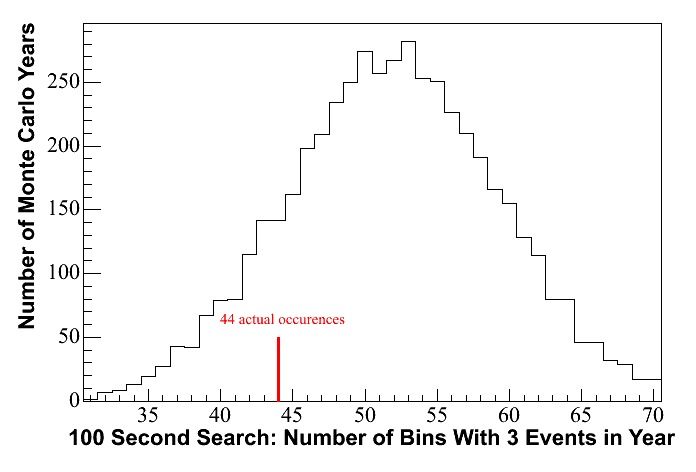
The maximum number of events observed in any bin in the 100 second search was 3 events. This is a slight downward fluctuation from expectation: the maximum number of events in any bin is predicted to be 4 over 75% of the time. There were 44 total time windows throughout the year with 3 events, which is well within the range of expectations. The plot below shows the breakdown of the number of bins with 3 events in a year according to Monte Carlo.

In the 1 second search, the maximum number of events observed in any bin was also 3. The most probable value for a maximum in this search was 2, but the odds of getting 3 or more events just from background fluctuations in a bin are 20.1%, so this does not represent a statistically significant fluctuation. The sole bin with 3 events occurs on April 29th, in run 3202. This is neither in coincidence with a gamma-ray detection nor with a bin containing 3 events in the 100 second search.

The upper limit on flux from an ensemble of 667 bursts is ~2 X 10^-6 Gev/cm²ssr based on the 100 second search, before systematics are taken into account.

Original Unblinding page:

The following menu provides an overview of the webpage. In some cases, a summary of the topic is given on this main page, with a link provided for a more detailed explanation of the subject. Since the previous iteration of this proposal, cut selection and sensitivity calculation have been re-evaluated to optimize for discovery at the 5 sigma level. Additionally, tau and muon induced cascades have been integrated into the analysis, Arvid Pohl's flarechecker program has been used to check for flary events, the muon fit has been adjusted to ensure reproducibility of results and checks for a signal coincident with a gamma-ray satellite detection have been defined.

General Discussion
Proposal
Overview
Comparison with Other Searches
Time Window Choices

Data Processing and Cuts
Run Selection Criteria
Low Level Filtering
Data Reduction
Flarechecking
A Note on Reproducibility
Final Cut Selection
Additional Tests For a Significant Signal

Performance of Analysis
Sensitivity
Checks and Comparisons on Sensitivity
Stability Check Plots
Cascade Effective Volume and Neutrino Effective Area

General Discussion

Proposal

I am proposing to unblind the 2001 data set to perform a rolling search for a signal consistent with neutrino emission from a gamma ray burst.

Overview

The concept of the rolling search is a straightforward one: simply scan through all the data in a given year and search for a significant signal above background during a fixed time interval at any time during the year. The proposed rolling search is to be done in 2001 using the cascade channel and optimizing on a Waxman-Bahcall broken power law energy spectrum with break energies at 10⁵ GeV and 10⁷ GeV, consistent with expectations for a GRB neutrino signal from prompt emission. The signal Monte Carlo uses neutral current interactions for all three neutrino flavors and charged current interactions for electron and tau neutrinos. The specific method employed is to start at each event that survives cuts and check in a 100 second and 1 second time window following this event for other surviving events. Since a new search window is started at every surviving event, it is guaranteed that one will not miss a significant clumping of events. The significance of the largest cluster of events occuring during the year for both analyses will be evaluated. We will also check for two or three independent upward fluctuations which achieve a considerable level of significance when taken together, and for coincidence of a large cluster of events coincident with IPN3 (third interplanetary network) satellite detections.

Comparison with Other Searches

The rolling search is complimentary to other GRB searches conducted with AMANDA. Because there are no temporal or spatial constraints for the rolling search as in the satellite-coincident GRB searches such as those conducted by Kyler, Mike and Ignacio, multiple events within an individual fixed time window are required for a detection, a disadvantage compared to satellite-coincident searches. However, it is clear that the satellite-coincident searches miss a very large percentage of GRBs which occur. This is especially true in the post-BATSE era, including 2001, the data set being used for this search, because the remaining IPN3 satellites catch only a fraction of the bursts that BATSE detected. Therefore, the set of GRBs for which the rolling search can look is larger than is possible for a satellite-coincident analysis. In addition to the possibility of detecting a GRB missed by the satellite network, the rolling search may be capable of detecting gamma-ray dark phenomena, so the possibility of discovering new physics exists. Examples of phenomena without detectable gamma-ray signatures include neutrinos from "choked" gamma-ray dark bursts and neutrinos from mildly relativistic jets in non-GRB supernovae. Although both of these phenomena have neutrino energy spectra predictions that peak below energies to which this analysis is designed for, signal retention is still non-negligible for these phenomena (about 20% as efficient as for prompt emission spectra). In the future, it may be worth pursuing a new set of cuts which is designed for these lower energy phenomena, but the current analysis is optimized for high energy (~100 TeV) neutrino emission.

Time Window Choices

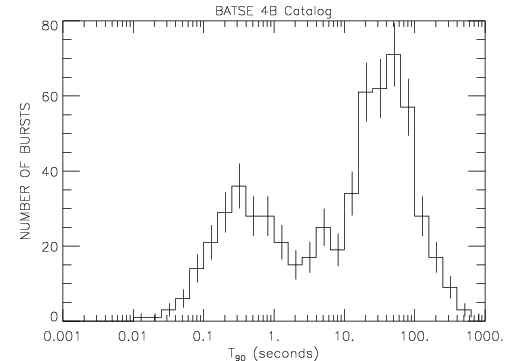
We will conduct two simultaneous searches, one with a rolling time window of 1 second and one with a rolling time window of 100 seconds. This is because the duration of gamma ray bursts follows a bimodal distribution, with one peak at times below 1 second for "short" bursts and the other, somewhat larger peak for "long" bursts. This bimodal distribution can be seen below for bursts from the BATSE catalog. Although a small percentage of bursts have durations longer than 100 seconds, this length was found to be the best trade-off between minimizing background and maintaining signal.

home

Data Processing and Cuts

Run Selection Criteria

Very short runs, runs which were marked as "special runs" on the 2001 monitoring page were left out of the analysis. Runs taken during the austral summer when the station was open were also excluded to ensure a stable data set. Additionally, runs 3111, 3112 and 3258, which showed very abnormal nch distributions and abnormal event rates were excluded. This left 226 runs which were within a few seconds of a full day duration and 12 additional runs of at least 30000 seconds, totalling approximately 233 days total time running. The list of runs used in this analysis was cross-checked against the 2001 runs from the Zeuthen 4 year sample as well as their bad file list and it was verified that no files are to be used in this analysis that were not used in the 4 year sample. A complete list of runs used can be found here.

Reconstructions and Low Level Filtering

The high energy data stream for 2001 data at UW Madison was used for the real data. Hit cleaning is thus identical to other analyses using the 2001 filtering at Madison. Lists of hit cleaning TOT cuts, X-talk fits and bad OMs are available. Cascade and muon reconstructions were done using upandel fits.

Data Reduction

Data reduction is accomplished in three steps: a high energy filter which cuts on nhits and the number of hit OMs with 2 or more hits, followed by a loose cut on the ndirect variable, and finally an optimized cut on the output of a six-variable support vector machine. Details of data reduction, which have not changed since the previous iteration of this unblinding proposal, can be found here.

Flarechecking

Arvid Pohl's flarechecker has been run on all files to be used in this analysis. Flarechecking was done at the high energy filter level, but before any other cuts. Based on observation of the distributions, the flare cut applied will be Induc_B10<7 and Induc_11<5. These variables eliminate all obviously flary events and maintain 100% of the signal Monte Carlo. Run 3399 will be excluded entirely because of its high flare rate. For more details and plots, click this link.

A Note on Reproducibility

The iterative muon fit (used in the nlate, ndirect and likelihood ratio cuts) displays the same unreliable behavior observed in other high energy analyses, including Lisa's UHE search. While the overall distributions of variables based on this fit are reliable, individual high-energy cascade-like events may have significantly different results when the same fit is re-run with a different initial random number seed. While one shouldn't expect track-like fits to work very well on my high energy cascade signal, this raises the problem that if the reconstruction is re-run for some reason, a non-negligible number of events may fluctuate between "signal" and "background" classifications. The iterative muon fit has therefore been re-run using a version of recoos with a user-defined random seed, which ensures reproducibility of my results.

Final cut selection

    Since our sensitivity will be higher than other analyses for conventional GRBs, we have decided to optimize for discovery rather than sensitivity. In the end, however, our discovery-optimized cuts lead to sensitivities less than 8% above the optimal sensitivity for both searches.
    The observable used to determine Model Rejection Potential and Model Discovery Potential values is the largest number of events present in any time window during the year. This means that, although we will check for the presence of multiple bursts in the year, our cut selection is based on optimizing for greatest likelihood of discovery of a single burst. Specifically, we optimize so that we have a 90% chance of seeing a signal with at least 5 sigma significance from the lowest possible signal flux.
    When using a support vector machine, the tightness of cuts is optimized by selecting the correct "cost factor", with smaller cost factors corresponding to tighter cuts. A cost factor of .08 (80.9% signal retention) was found to be optimal for the 100 second search, while a cost factor of .45 (96.0% signal retention) was optimal for the 1 second search. 8 events would be required in a 100 second window or 5 events in a 1 second window would be required to obtain a signal above 5 sigma significance. The two plots below show output from the support vector machine for signal Monte Carlo of all three flavors with proper weighting for the support vector machine cost factors selected for the 1 and 100 second searches, respectively. Kept events are to the right of the green line. Much greater detail concerning the cut selection process is available for people who like statistics.

home

Additional Tests for the Presence of a Significant Signal

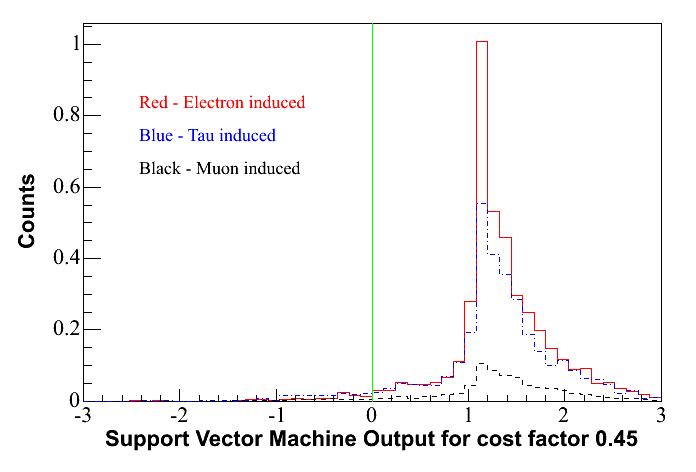
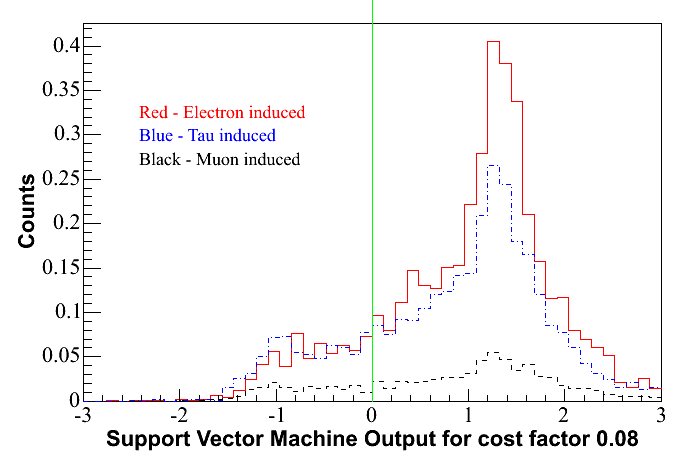
I. 2 or 3 Separate Marginal Detections

In the event that we fail to detect a 5 sigma signal from an individual burst, we can also check for 2 or 3 independent "borderline" detections. These would result from 2 or 3 bursts happening at different times throughout the year which don't generate enough events to be an unambiguous signal on their own, but when taken together, have a large statistical significance. Checking for these causes a small reduction in the significance of an observation because it increases the "trials factor". However, making this check does increase our odds of seeing something. An exhaustive pre-defined list of the combinations resulting in greater than a 5 sigma significance follows:

combination of events (total number of independent bursts in parentheses)	chance probability due to background fluctuation
8 or more events in a single bin in the 100 second search (1)	1.12 X 10^-7
5 or more events in a single bin in the 1 second search (1)	1.65 X 10^-7
One bin with 7 events and one bin with 6 or 7 events in the 100 second search (2)	5.15 X 10^-9
Two or more bins with 4 events in the 1 second search (2)	5.15 X 10^-8
One bin with 7 events in the 100 second search and one bin with 4 events in the 1 second search (2)	1.97 X 10^-9
Two bins with 6 events and one other bin with 5 or 6 events in the 100 second search (3)	1.15 X 10^-8
One bin with at least 6 events and one bin with 5 or 6 in the 100 second search and one bin with 4 events in the 1 second search (3)	4.45 X 10^-9

Each burst must be completely independent for it to count (i.e. two bursts cannot share any events, otherwise it is assumed they are in fact the same burst). Similar checks will be made for 4 sigma or 3 sigma significance assuming no 5 sigma detection is found (scroll down to Total Probability of a False Detection for these comprehensive lists).

II. Comparison with IPN3 burst detection times

In the event that we obtain 7 events in a bin from the 100 second search or 4 events in a bin from the 1 second search, we will then compare the time at which this upward fluctuation occurs with the times of GRBs identified by the third interplanetary network, IPN3 . If the duration of the burst is found to overlap with the duration of the time window with this high number of events, this will then be a statistically significant observation. The thresholds of 7 events and 4 events were selected because the probability of this many events in a time window occurring due to background fluctuations and in coincidence with a satellite observation is sufficiently small that we can claim 5 sigma significance if this occurs. For example, in the 1 second search, the odds of getting 4 or more events in a time window at some point during the year are 2.3 X 10^-4. The odds of this time window occuring in coincidence with a GRB detection are 1.1 X 10^-4, so the total odds of getting 4 or more events in coincidence with a GRB are 2.3 X 10^-4 * 1.1 X 10^-4 = 2.5 X 10^-8, considerably below the 5 sigma threshold of 6 X 10^-7. Lower numbers of events in coincidence with a GRB do not meet this standard for significance, but assuming we fail to make a 5 sigma discovery, we will check for a cluster of 6 or 5 events in the 100 second search coincident with a satellite detection, as these would merit a significance greater than 4 sigma or 3 sigma, respectively.

I have compiled a list of 78 detections by the IPN network. Unfortunately, the majority of these triggers are from the Konus-Wind experiment and do not have reliable durations (or localizations, although this isn't a problem in my case). For those bursts for which other information is not available, I have estimated durations based on lightcurves provided by Konus-Wind. These estimates are probably systematically lower than BATSE T₉₀ times, based on comparisons with the BATSE sample from Ignacio's analysis. The durations of many of these bursts are probably not reliable enough for a conventional satellite-coincident analysis, but will be used here as they are the only thing available. An OpenOffice spreadsheet is available with burst times and approximate durations. A time window will be defined as in coincidence with one of these bursts if any portion of the bin overlaps with any portion of the burst, allowing 1 second before the trigger.

Total Probability of a False Detection

Scenario resulting in a discovery of at least 5 sigma significance	Chance Probability Due to Background Fluctuation
8 or more events in a single bin in 100 second search	1.12 X 10 ^-7
5 or more events in a single bin in 1 second search	1.65 X 10^-7
Combinations of 2 or 3 bursts	0.75 X 10^-7
8 events from 100 second search in coincidence with satellite detection	0.08 X 10^-7
5 events from 1 second search in coincidence with satellite detection	0.25 X 10^-7
Total	3.85 X 10^-7

The observation of any of the above scenarios would therefore have a significance of greater than 5 sigma (6 X 10^-7probability) after accounting for all trials. Of course, no discovery would be claimed until after the events have been examined and are determined to look like reasonable signal events. Similar charts for significances of 4 sigma and 3 sigma can be found by clicking this link. While a statistical significance of 3 or 4 sigma would not be sufficient to claim discovery, it would at least be an interesting observation.

Performance of Analysis

Sensitivity

Sensitivity for this analysis is determined to be 2.7 X 10^-6 GeV/cm²ssr, assuming a diffuse flux resulting from 667 bursts, derived from the rate of observations by the BATSE satellite, of which ~425 are during the on-time for this analysis. This is an all flavor limit, assuming a flux ratio of 1:1:1 at Earth. This result does not take into account systematics, although deadtime of 21.4% has been included. This calculation also assumes an expected event rate that varies from burst to burst according to the predictions in Guetta et al. For more information on this "Guetta" distribution, click here. If one assumes a "flat" distribution, with equal flux per burst, one obtains a sensitivity of 1.3 X 10^-5 GeV/cm²ssr. The improvement from using the more realistic distribution results from the fact that one is more likely to obtain a cluster of events from the same total flux when a large percentage of that total flux is contained within a few bursts than when it is spread out evenly. An overview of the procedure used to do my sensitivity calculations can be found here.

Checks and Comparisons of my Sensitivity

I. Comparison with Ignacio's satellite-coincident search

I supposed that I had a situation identical to Ignacio's year 2000 analysis: 74 bursts with known durations and times, with total on-source time equal to 2822.5 seconds. This hypothetical situation allows a useful check on my cuts and sensitivity calculations. I re-optimized my support vector machine cut (using average background rates) but kept the filtering the same, counting total events during all 74 periods, rather than clusters as in my rolling search. Using my cuts, my optimal sensitivity was 6.2 X 10^-7GeV/cm²ssr (with deadtime correction) for a satellite-coincident GRB search with 74 bursts. Since Ignacio's sensitivity of 9.5 X 10^-7 GeV/cm²ssr is 30% above his optimal sensitivity (because he optimized for discovery) and because one generally expects somewhat better sensitivities from 2001 analyses compared to 2000 analyses due to the larger number of OMs that could be used, these values are within the range of agreement one would expect. My effective volume is considerably larger (even adjusting for differences in year) because my cuts were explicitly designed to maximize effective volume by utilizing uncontained as well as contained events, but this also allows in considerably more background, increasing my average upper limit, so the net effect on sensitivity of choosing this method ultimately appears to be fairly minimal, at least in this case.

II. Back-of-the-envelope sensitivity check

Mathematically, a 90% C.L. sensitivity calculation is different than determining the flux at which one has a 90% chance of seeing something above background. However, one expects they should generally have similar values. The following is a back-of-the-envelope check which calculates the flux at which one has a 90% of seeing a fluctuation above background assuming 425 identical bursts, which should correspond roughly to the sensitivity of 1.3 X 10^-5 GeV/cm²ssr which one obtains when assuming equal flux for each burst.

To have a probability of .9 of detecting a signal, one has a .1 probability of failing to detect a signal. If there are 425 equivalent bursts, then statistically, the odds of failing to detect any bursts is just the product of the probabilities of the failure to detect each burst individually. Thus:

where p is the probability of not detecting one individual burst. Since 5 events is outside the 90% confidence belt at 0 events, 5 or more events is above background for the purposes of this calculation, even though this would not be significant enough to label it a discovery. Assuming Poissonian statistics and counting 5 or more events as a "signal", the odds of failing to detect an individual burst with signal expectation lambda is simply the odds of obtaining 4 or fewer events:

When solving for lambda, one obtains an expectation of 1.1 events per burst. Multiplying this by the total expected number of bursts per year, 667, one obtains an expectation of 733.7 events. One can then scale this with the total number of events one obtains from ANIS given a total flux of 4.5 X 10^-9 GeV/cm²ssr (summed events from e, mu and tau with 1.5 X10^-9 flux each), which is .323, to scale up to the flux we are sensitive to.

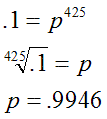
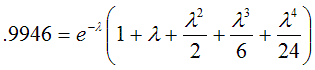
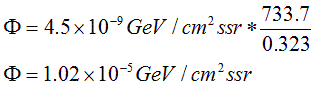
After correcting for deadtime, one obtains 1.3 X 10^-5, identical to the sensitivity determined for the flat model.

Stability Check Plots

Several checks have been made to verify that the data after cuts is consistent with expectations. Delta-t plots showing that real data is consistent with Poissonian predictions, background rate plots showing consistent rates throughout the entire year and plots showing that the number of times two events occur in a time window during a year using real data is consistent with Monte Carlo predictions are all available here.

Cascade Effective Volume and Neutrino Effective Area

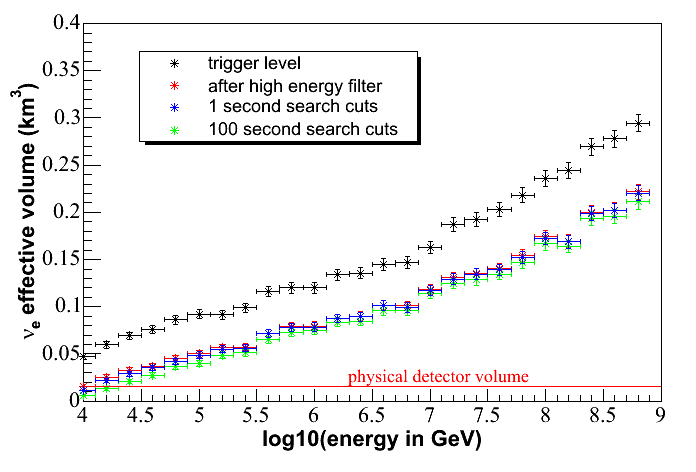
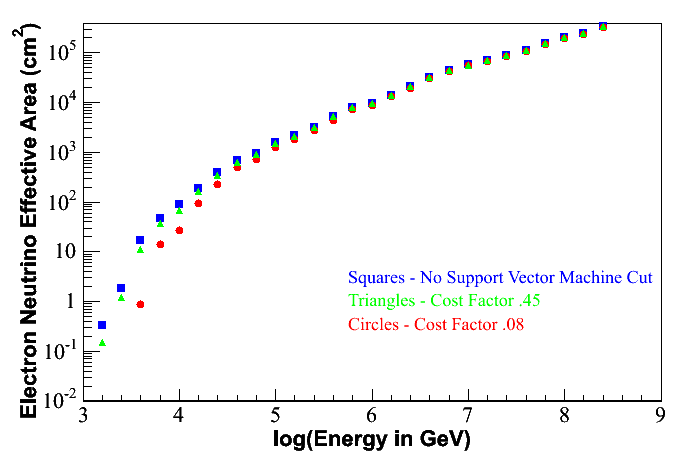
Cascade Effective Volume and Neutrino Effective Area plots are shown below for electron neutrino events. Plots for tau events are also available, but they look very similar to the electron neutrino plots. Muon neutral current events also contribute, but these are a small percentage of the total signal. The effective cascade volume plots demonstrate the advantage of utilizing uncontained events, especially at high energies.

efvol.elec.gif

effarea.elec.gif

Shown below is a plot with the input signal spectrum folded with effective area functions for no support vector machine cut and the cuts used for the two searches. This gives the distribution of energies expected for detected events, assuming the initial input spectrum parameters. (The Glashow resonance was included in the actual signal MC used, but does not appear in the plot below.)

home