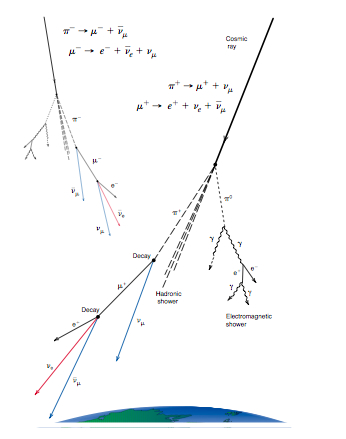
Figure 1: Atmospheric neutrino production, from Los Alamos Science 25 (1997).
John Kelley, UW-Madison, September 2005

Figure 1: Atmospheric neutrino production, from Los Alamos
Science 25 (1997).
AMANDA-II has now accumulated a large sample of high-energy atmospheric muon neutrino events. While considered a background to many analyses (such as point source searches), these atmospheric neutrinos provide a unique means of testing physics beyond the Standard Model. A number of proposed models predict effects in the neutrino sector that result in a distorted atmospheric energy / zenith-angle spectrum. AMANDA-II should be able to probe beyond the best current limits on some of these new physics (NP) effects by an order of magnitude or more.
These effects are detectable by the same method as standard neutrino oscillations — muon neutrinos generated in the atmosphere change flavor as they propagate to the detector. Because of the different path lengths at different zenith angles, this results in a measurable distortion from the expected zenith angle / energy spectrum. Unlike standard atmospheric oscillations, which decrease with energy and are essentially negligible above 100 GeV, these effects often increase with energy (depending on the model — see figure 2).
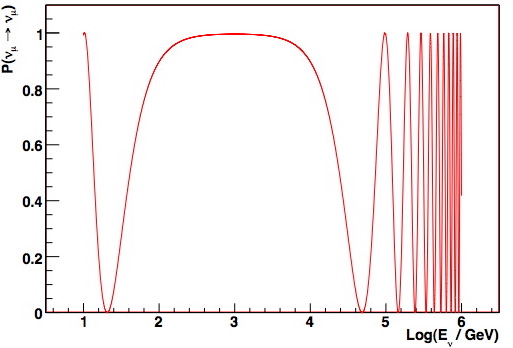
Figure 2: Survival probability for vertically
upgoing muon neutrinos, VLI oscillations*, deltac/c
= 1e-27.
Conventional oscillation effects are still observable at low energies.
Specific models that can be tested with this techniques include violations of Lorentz invariance (VLI) resulting from different limiting neutrino velocities, and violations of the equivalence principle (VEP) due to non-universal coupling of the neutrinos to the gravitational field. Both of these are described in Gonzalez-Garcia, Halzen, and Maltoni (hep-ph/0502223), along with the sensitivity of IceCube to the effects. Neutrinos in a flavor eigenstate may also decohere into a mixed state through interactions with a foamy quantum-gravitational space-time. The phenomenology of these quantum decoherence effects is described in Morgan et al. (astro-ph/0412618), including the sensitivity of the ANTARES detector.
Additional background and theoretical motivation of Lorentz violations is presented in Coleman and Glashow (PRD 59 (1999) 116008) as well as Glashow (hep-ph/0407087). Additional background on quantum decoherence is available in Ellis et al. (Nucl. Phys. B241 (1984) 381-405) and Anchordoqui et al. (hep-ph/0506168).
AMANDA-II data from 2000-2005 will be used for this analysis. For 2000-04, the unified Zeuthen filtering (see this page for 2000-03, and this page for 2004) will be used up to Level 4, after which analysis-specific cuts will be defined, optimized to isolate atmospheric neutrinos from mis-reconstructed downgoing muons. The Mainz group (in particular, Thomas Becka and Jens Ahrens) have already devoted a significant amount of effort to this and have achieved quite impressive efficiencies. See T. Becka's web page for more information. We anticipate that this analysis will be complementary to the ongoing analyses of the Mainz group.
Blindness is an important and somewhat difficult topic when it comes to an atmospheric neutrino analysis. Discussions with Paolo Desiati and Lutz Koepke on this issue resulted in a general consensus that the best approach involves using cuts which select only for track quality, such as smoothness, paraboloid fit error, and likelihood ratio, and specifically avoiding variables affected by the new physics effect. In particular, since "disagreement" between data and MC zenith angle distributions could be a signal, zenith angle and related variables should specifically be kept blinded.
The references listed in section 1 provide useful parameterizations to simulate the effects of oscillations due to VLI effects or quantum decoherence. Specifically, a muon neutrino survival probability based on energy, zenith angle, and the specific parameters of the new physics (NP) model can be used as an event weight atop a standard atmospheric neutrino model, including prompt contributions (such as the various alternatives available via the NeutrinoFlux class).
The following figures show the survival probability for VLI and quantum decoherence effects, as contour plots across energy and zenith angles.
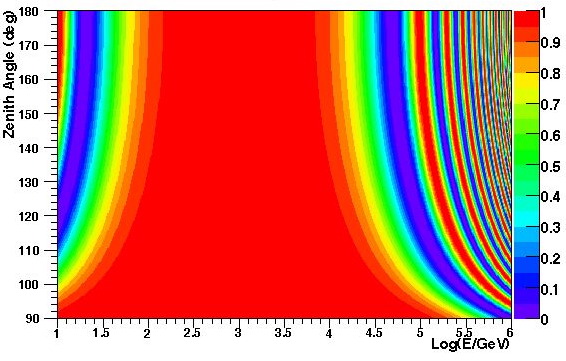
Figure 3: Muon neutrino survival probability as a function
of energy and zenith angle,
standard+VLI oscillations (deltac/c = 1e-27).
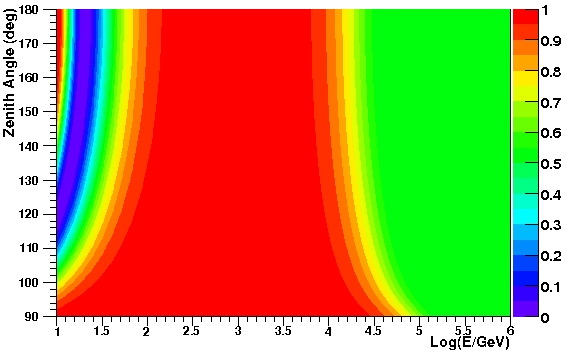
Figure 4: Muon neutrino survival probability
as a function of energy and zenith angle,
standard oscillations+decoherence ("kappa" model*,
a = alpha = 4e-32).
We plan on using Monte Carlo utilizing the photonics simulation framework.
We are starting with an analysis technique similar to the one described in hep-ph/0502223. This involves dividing the sky into two zenith angle ranges (one "horizontal" and one "vertical"), and constructing the following double-ratio:
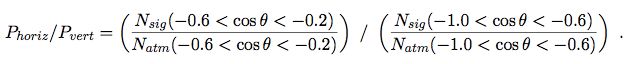
The signal, in this case, is an atmospheric model with standard oscillations and NP effects, and this is divided by the expectation with only standard oscillations. Note that the area just below the horizon can be excluded to avoid troublesome background contamination.
NP effects can cause this ratio, in certain energy ranges, can deviate significantly from unity. See figure 5 for two examples using VLI oscillations of various magnitudes.
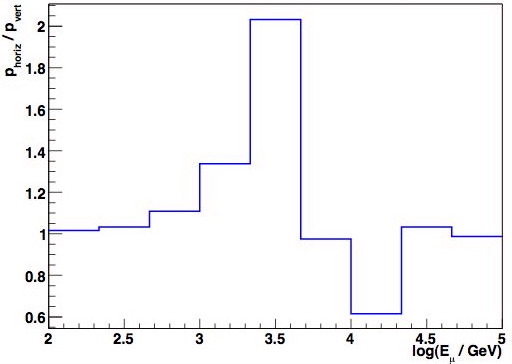 Figure 5a: MC double ratio vs. muon energy for VLI oscillations (deltac/c = 1e-26). |
 Figure 5b: MC double ratio vs. muon energy for VLI oscillations (deltac/c = 1e-27). |
Quantum decoherence also results in an observable effect, although the change in the double-ratio is less pronounced, because the high-energy effect is a damping term instead of an oscillatory one (see figure 6). An approach that doesn't eliminate all information about the normalization may be more advantageous in this case.
Figure 6: MC double ratio vs. muon energy for
quantum decoherence
("kappa" model, p_a = p_alpha = 4e-32).
Although we have used two zenith angle bins here, even for the VLI case this may be non-optimal. We plan to examine other zenith-angle ranges and binning to maximize the statistical power of the approach, à la the MACRO analysis in hep-ex/0106049.
Note that these plots were generated with non-optimal cuts (the Zeuthen point source cuts) and with a course binning in muon energy (30% in log E). Of course, examining this effect with real data will necessitate the use of a reasonably reliable energy estimator. Preliminary investigations using only the number of channels hit (Nch) are not promising, so a more sophisticated energy reconstruction will be employed. This is still under investigation.
Statistical methods are under investigation which will quantify the significance of any effect seen, or to map out an exclusion region in the NP parameter space, while correctly treating systematic uncertainties. The major advantage of using the double ratio is that systematic effects which result only in a normalization shift will cancel out. Systematic effects which distort the zenith angle spectrum, however, must be carefully taken into account.
Please feel free to contact me if you have any questions or comments.
*Technical note: for the VLI plots, we have assumed a maximal NP mixing angle of pi/4, and have taken the relative phase eta to be zero.
*Technical note 2: the "kappa" model has a decoherence parameter which grows with E^2. This is the model upon which we are likely to be able to place the strongest constraints.