AMANDA Monte Carlo Updates

• The exponential component is indeed part of the true SPE distribution (poorly amplified photoelectrons) and not noise
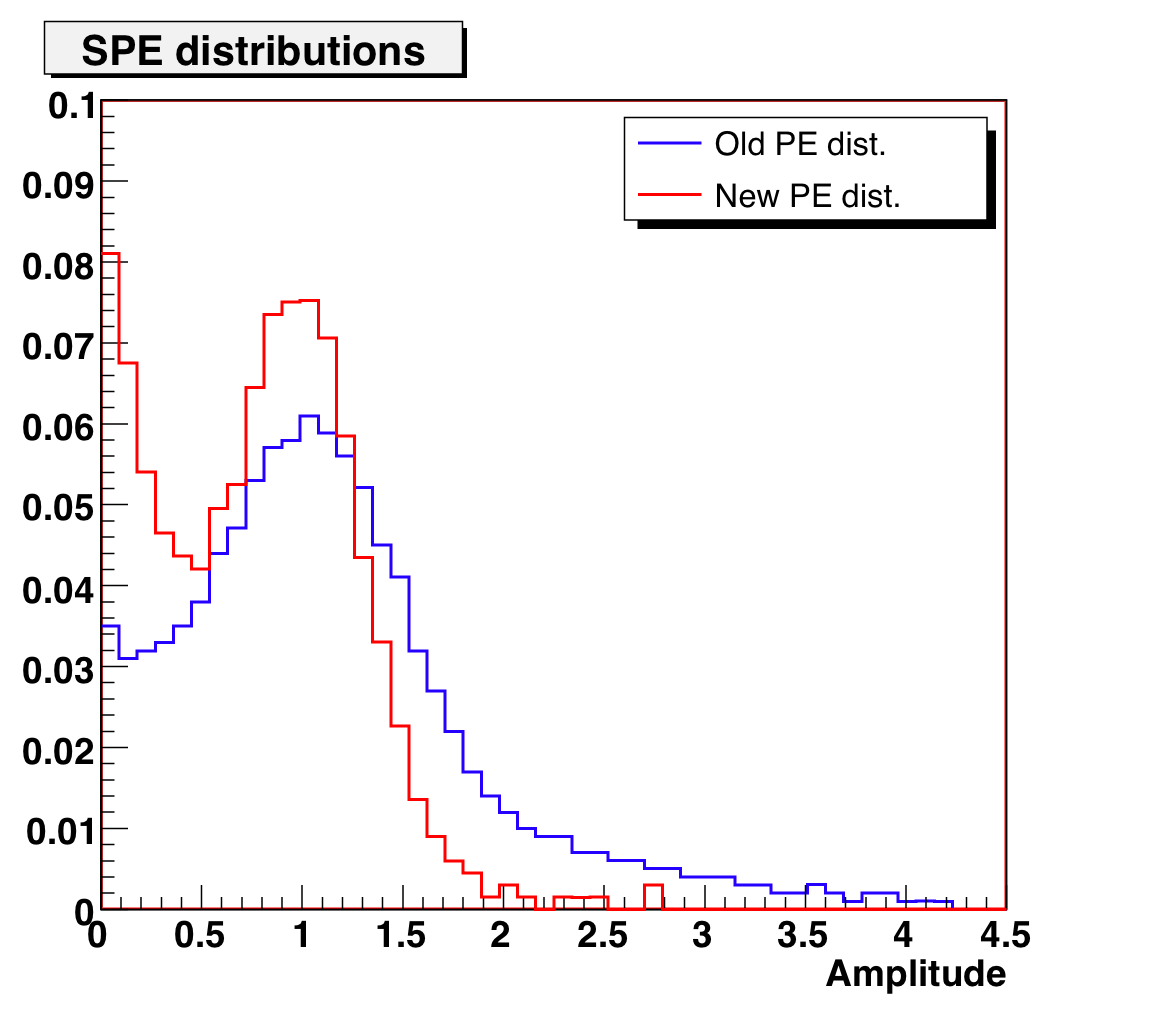
• The average SPE resolution as recorded in the monitoring data is somewhere between Stephan's PE distribution and the old one
• There is possibly a second, flatter exponential component responsible for the low-amplitude shoulder of the PE response (around 0.2 PE)

Using these findings, I also created a new PE distribution to test. The three PE distributions are shown below:

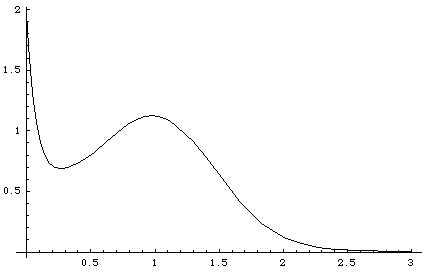
Figure 1: AMANDA SPE distributions for MC
(LEFT: original OM3 (blue), SH variant OM6 (red); RIGHT: JK dual exponential variant OM8)

The inverse CDF tables for use with Amasim are here:

• Original AMANDA (om3.einpe.ascii)
• SH variant (om6.einpe.ascii)
• JK variant (om8.einpe.ascii)

The proof is in the pudding, however, so MC simulations with each of these have been performed for comparison with 2005 data. The following parameters were fixed for this test:

• MC: dCORSIKA 6.6 + SIBYLL HE interaction model + Hoerandel spectrum
• canonical OM sensitivities (0.85 for B10, 1.0 others) unless mentioned
• Amasim aluminum-opt5
• AHA, Millennium, and PTD (mamint) ice models used as noted
• minimal 2005 filtering used (bad OM and modified xtalk cleaning, JAMS reconstruction, no quality cuts unless mentioned)
• 0.8 days of data filtered

Some comparisons with downgoing data are shown below.

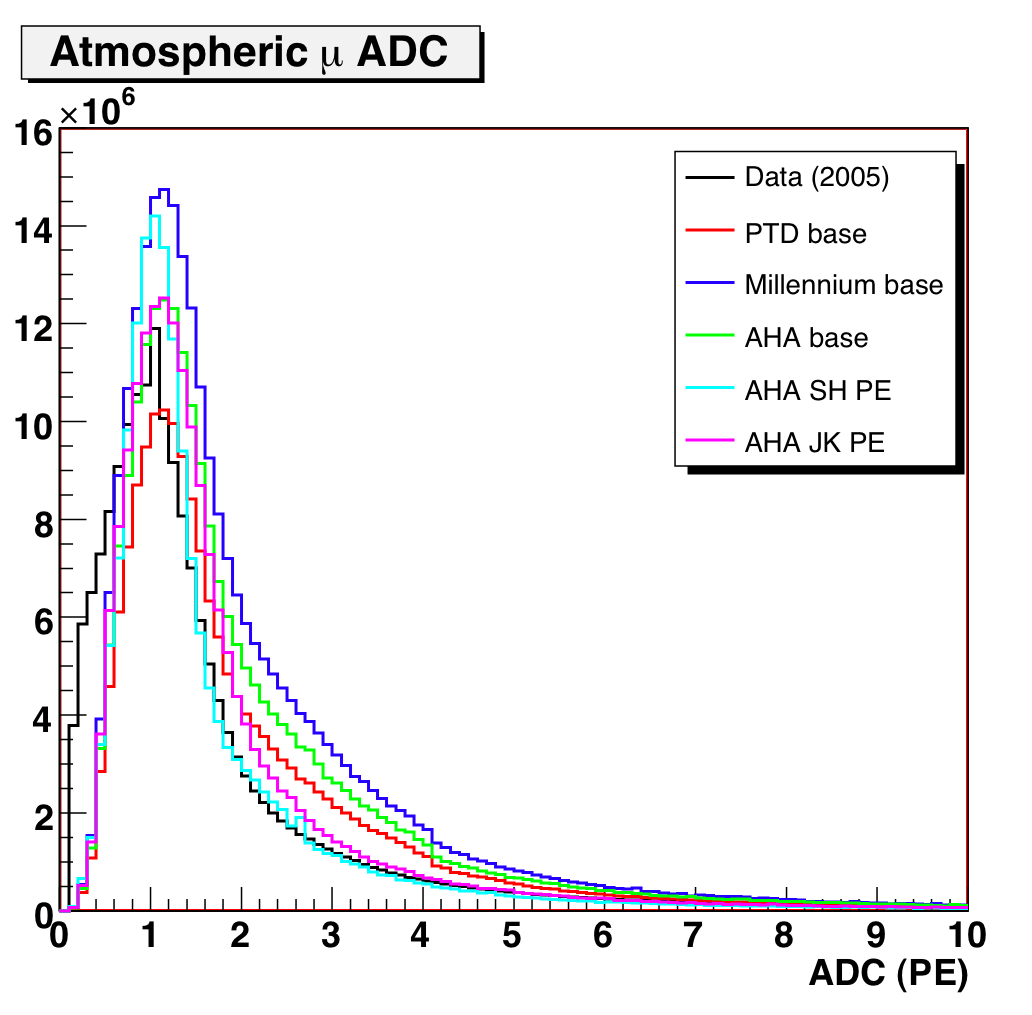
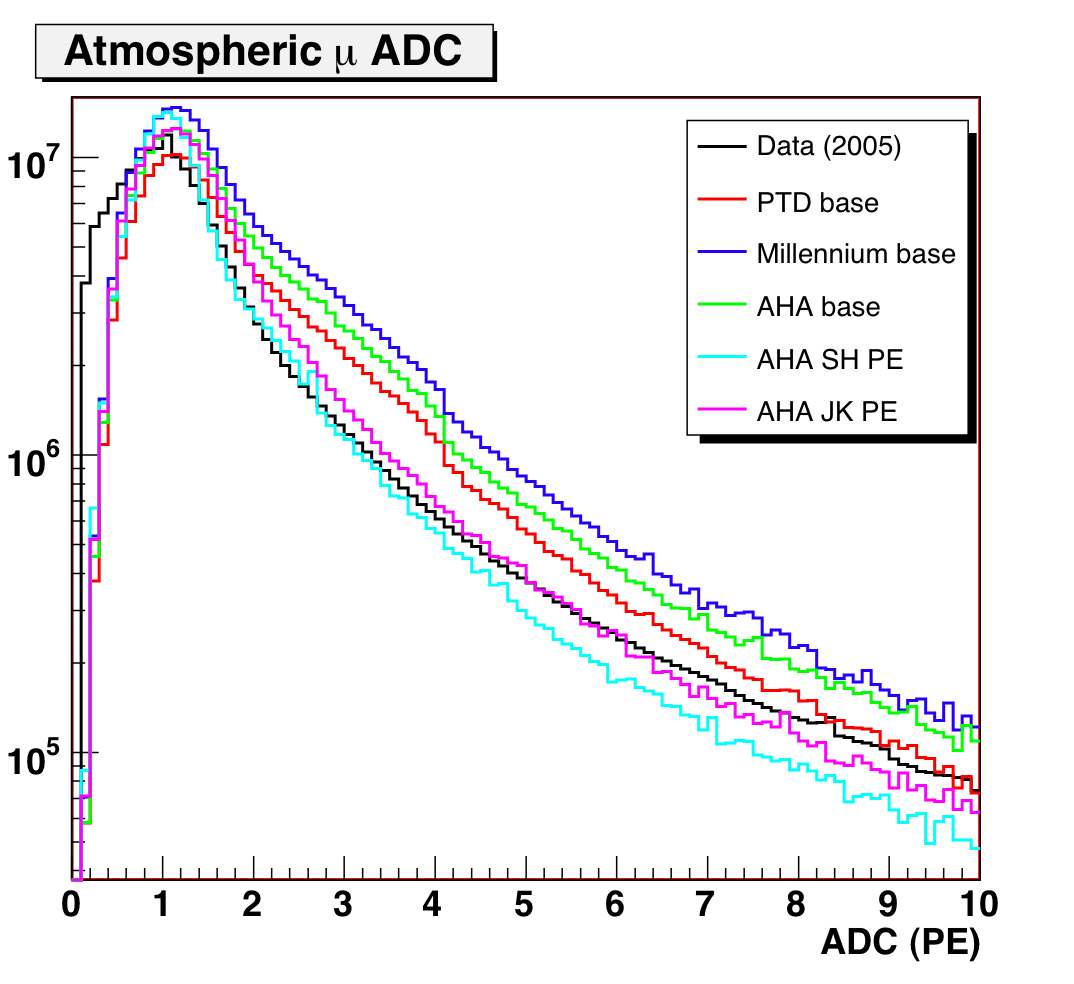
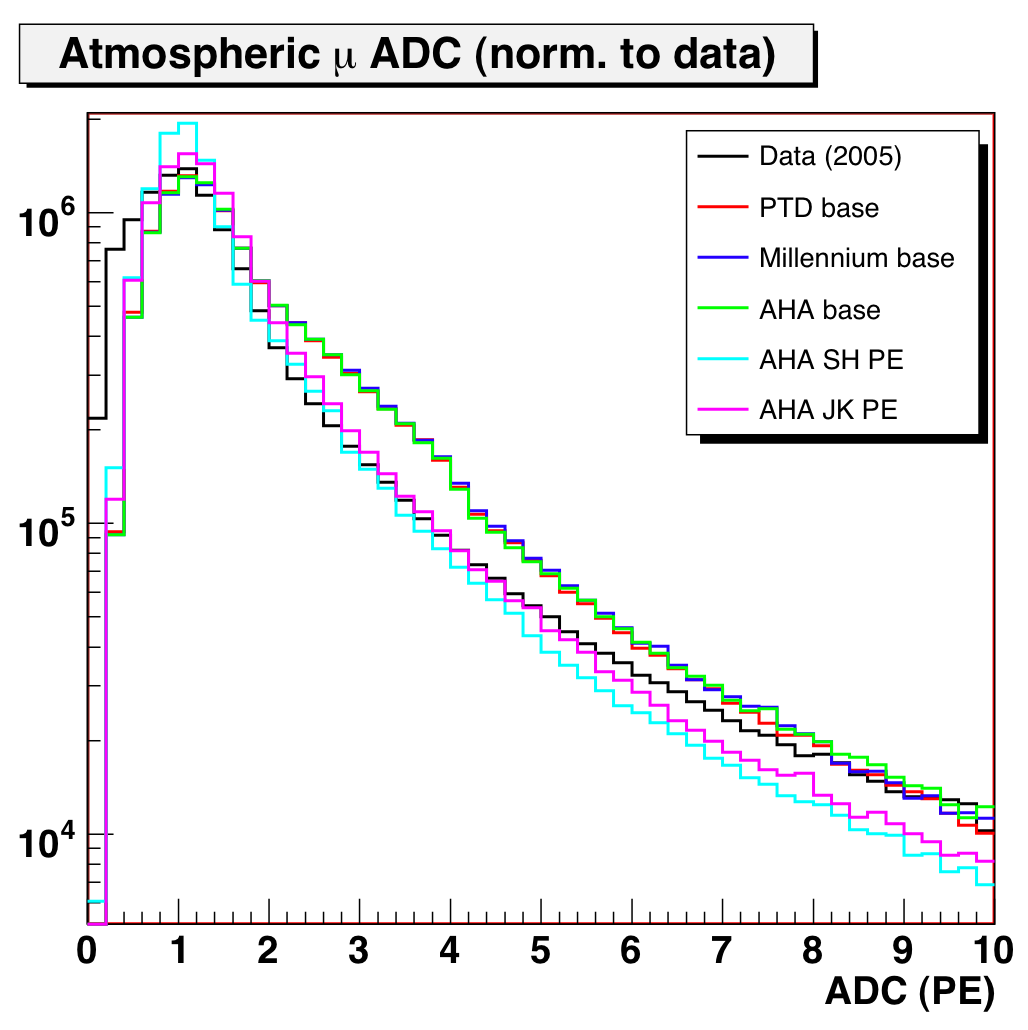
Figure 2: Downgoing muon ADC for 2005 data and MC. Left and center plots are normalized to livetime;
right plot is normalized to data to compare shapes.

Several things are notable about this comparison:

• No MC PE distribution reproduces the ADC spectrum of the data particularly well, especially at low amplitude
• The variant distributions (JK and SH) both look to be an improvement:
  SH does well in the 1.5-4 PE region, and in JK the peak shape is a little close to data (more rounded).
• The closest overall in shape is probably the JK variant (normalized plot on far right) — but it diverges at high ADC
• The shape of the ADC distribution is largely independent of ice

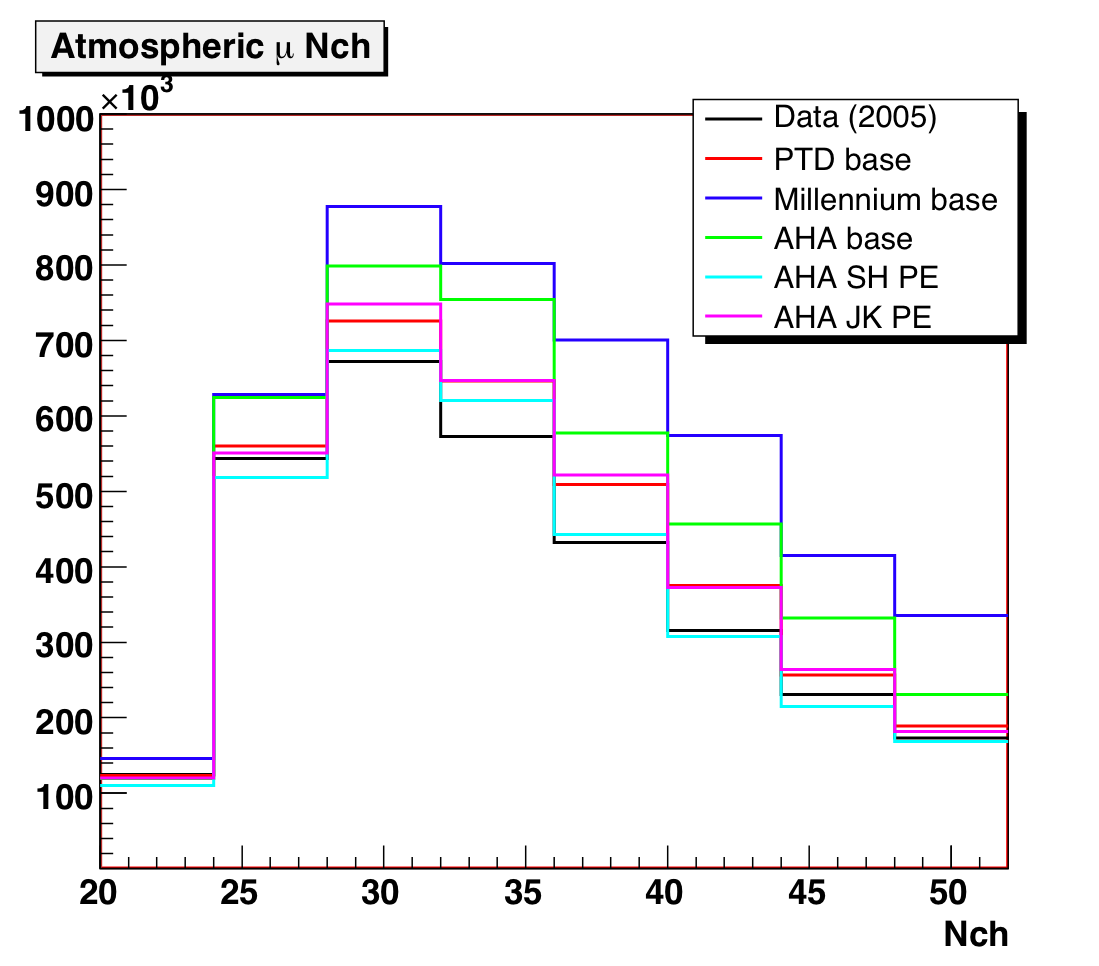
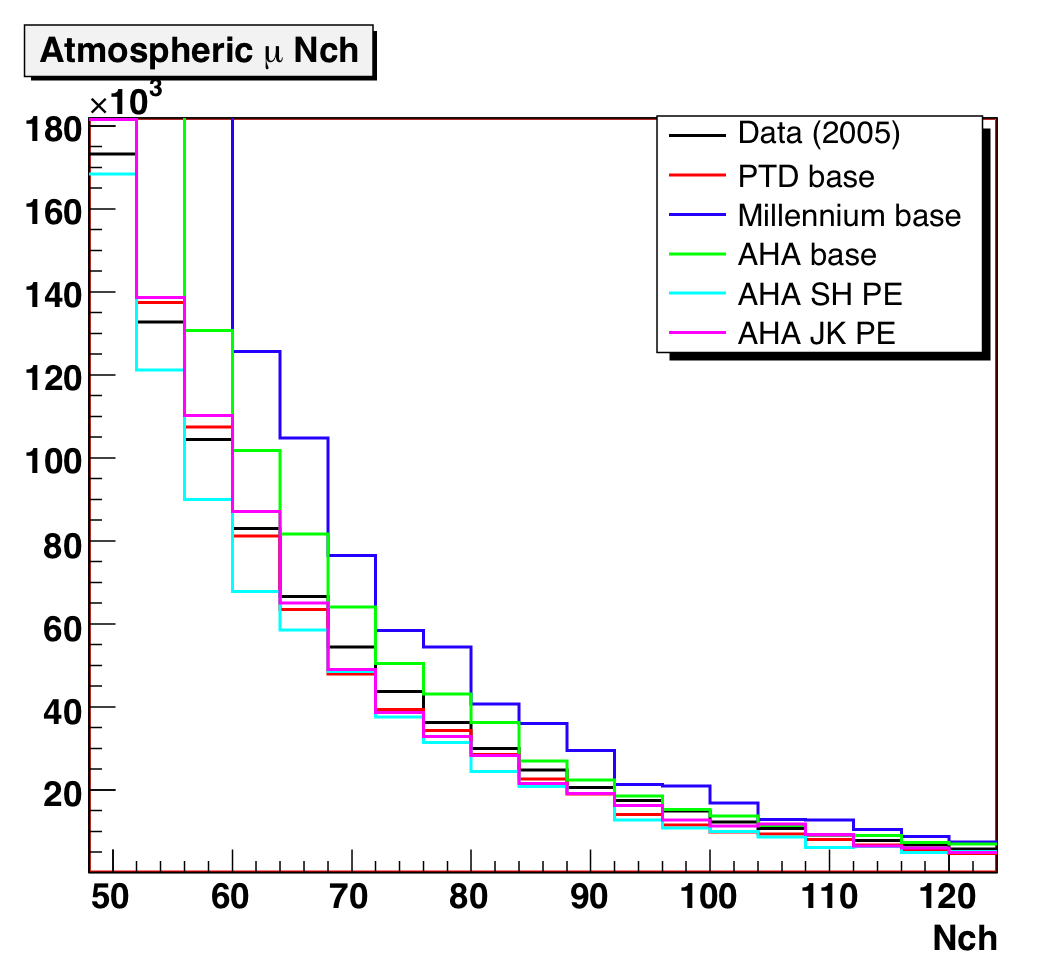
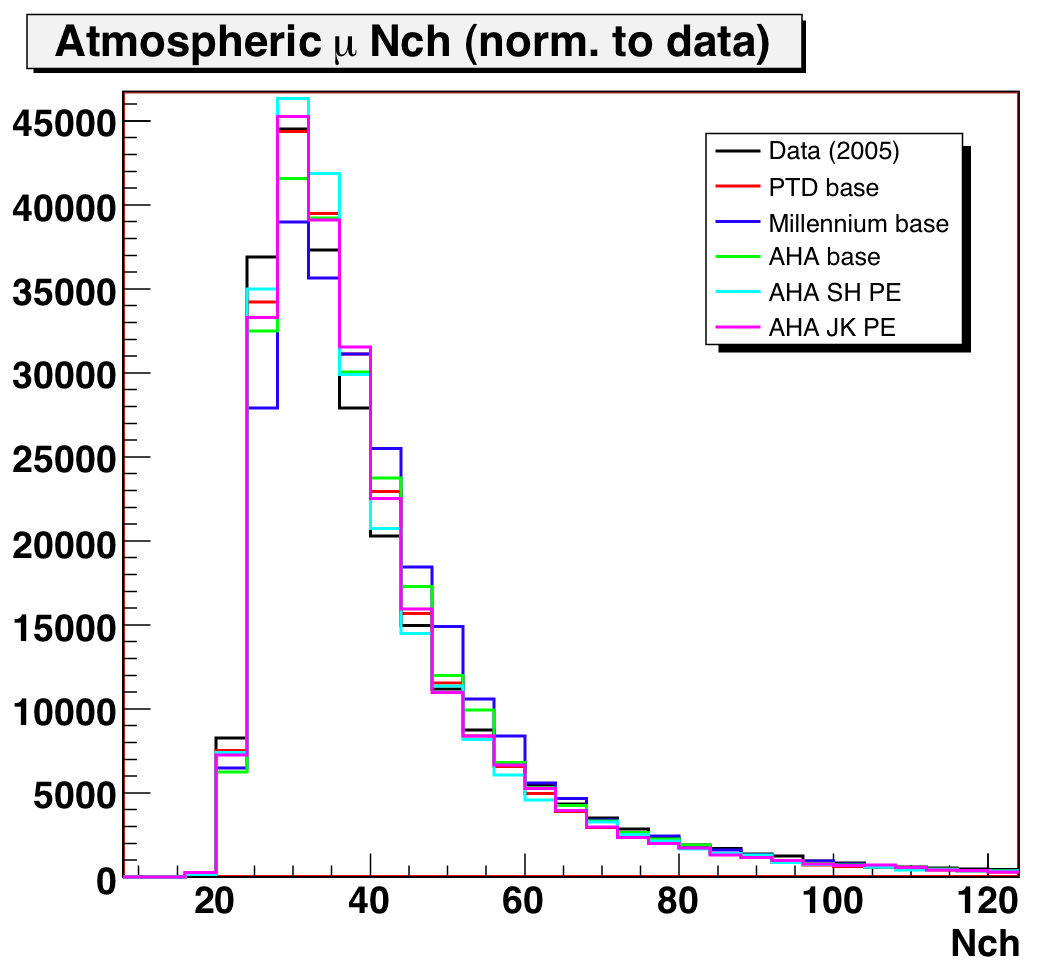
Here we plot the number of OMs hit, along with the weighted event counts:

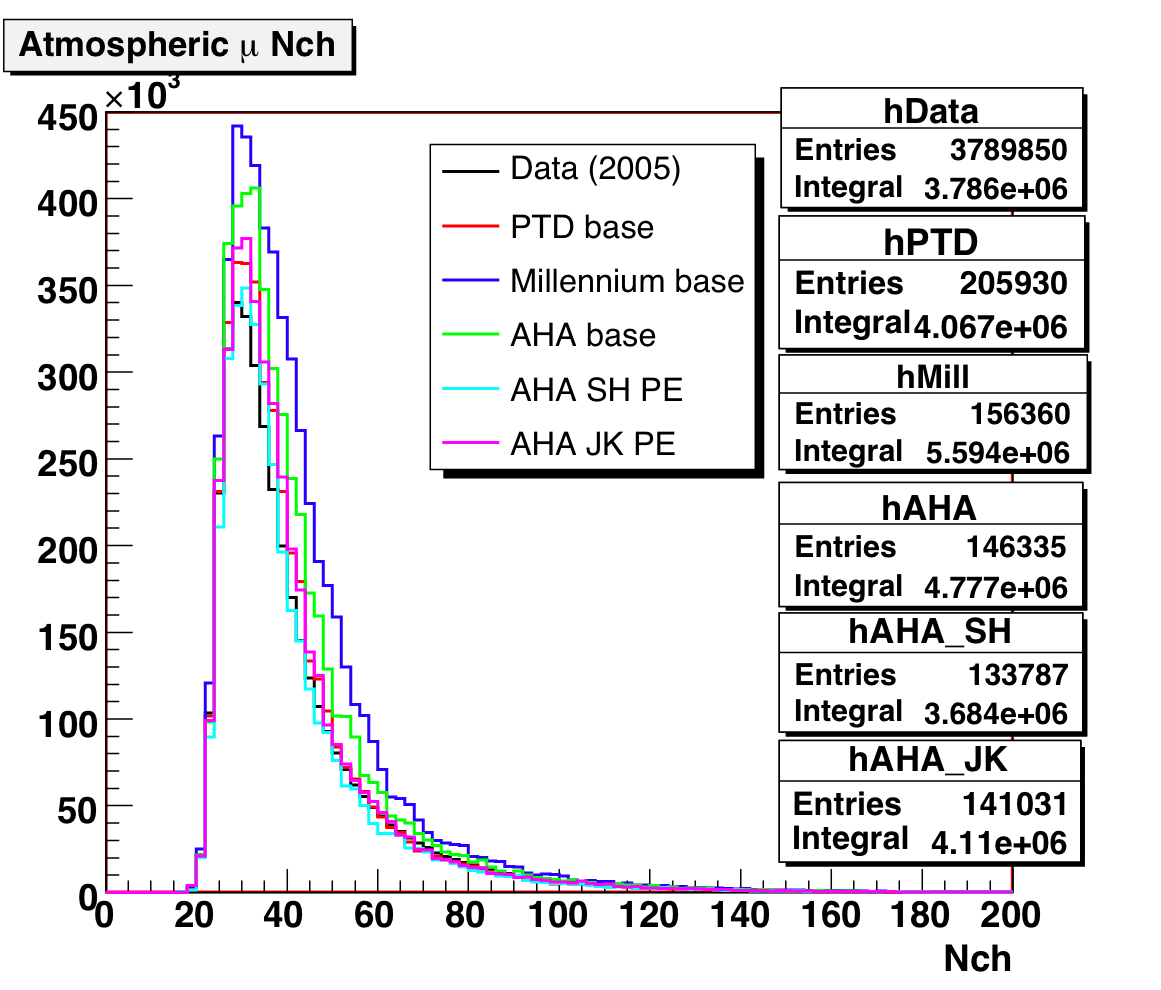
Figure 3a: Downgoing muon Nchannel data/MC comparison, for different ice and PE distributions.

Figure 3b: Downgoing muon Nchannel data/MC comparison (linear and log scales).
Left and center plots normalized to livetime; right plot normalized to data.

AHA with the SH PE distribution and old OM sensitivities is the closest to data in normalization: however, the initial negative slope seems to be a bit off. The JK PE distribution is next closest in normalization.

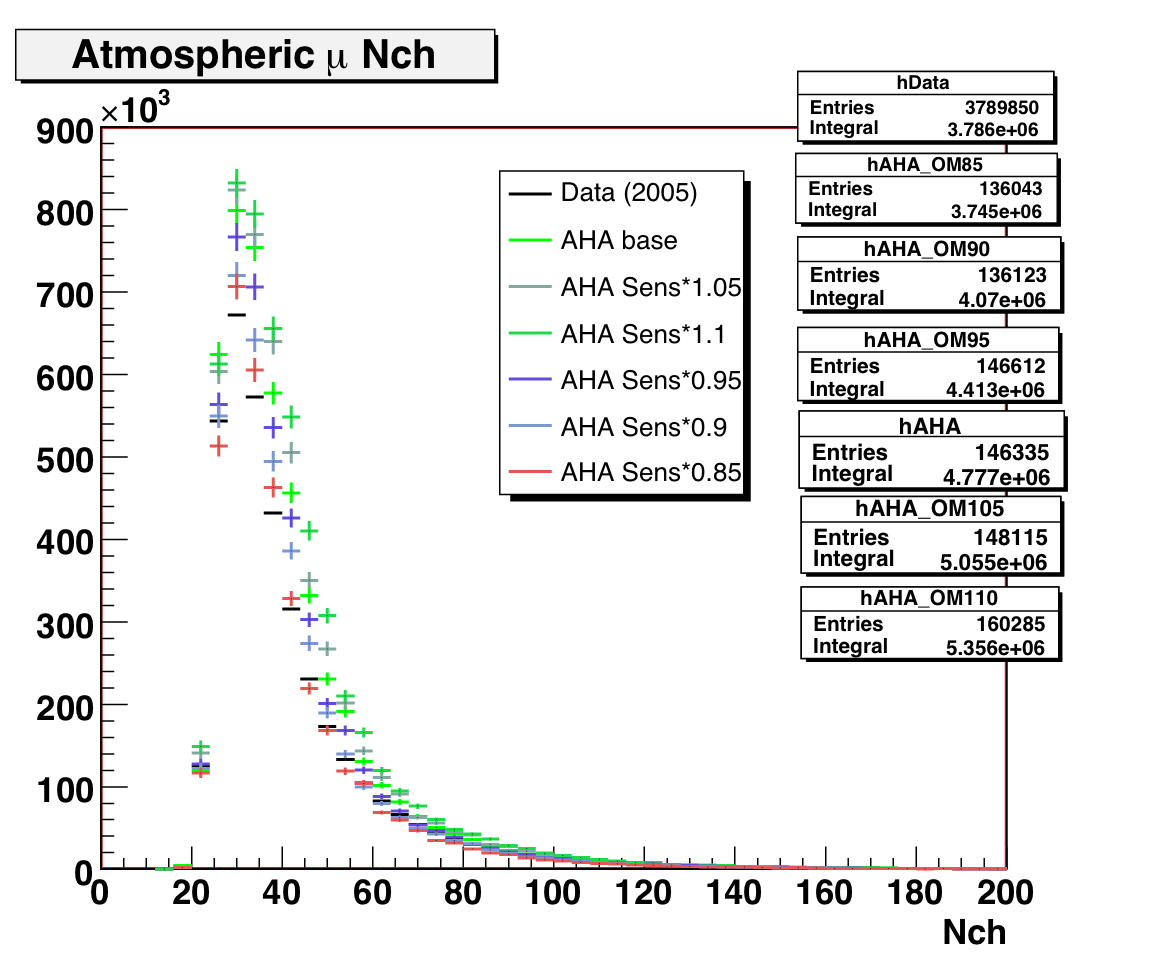
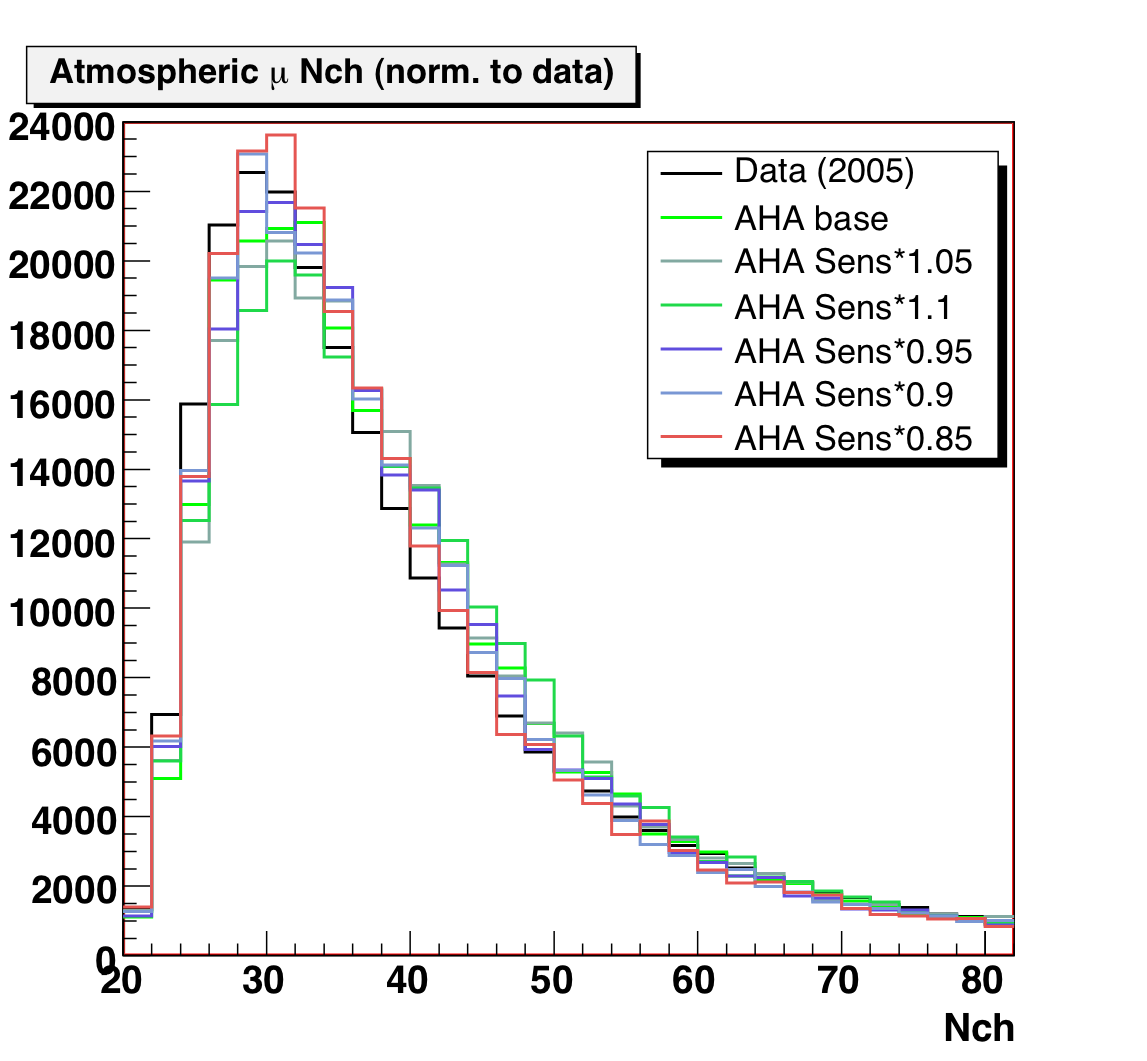
3. OM Sensitivity

We have also generated AHA dCORSIKA with a spread of OM sensitivities (changing the normalization, not tuning the individual OMs). Some results are shown below. Matching the peak position and low-Nch shape, as well as the normlization, suggests reducing the OM sensitivity. We will also tune the individual OM relative sensitivities with downgoing muons.

Figure 4: Downgoing muon Nchannel data/MC comparison for different OM sensitivities (linear and log scales).
Left plot normalized to livetime; right plot normalized to data.

A plot of reconstructed zenith angle is shown in figure 5. The shape (and normalization in previous plots) appear most consistent for 85% sensitivity, but no model matches the vertical events well (perhaps tighter cuts are needed).

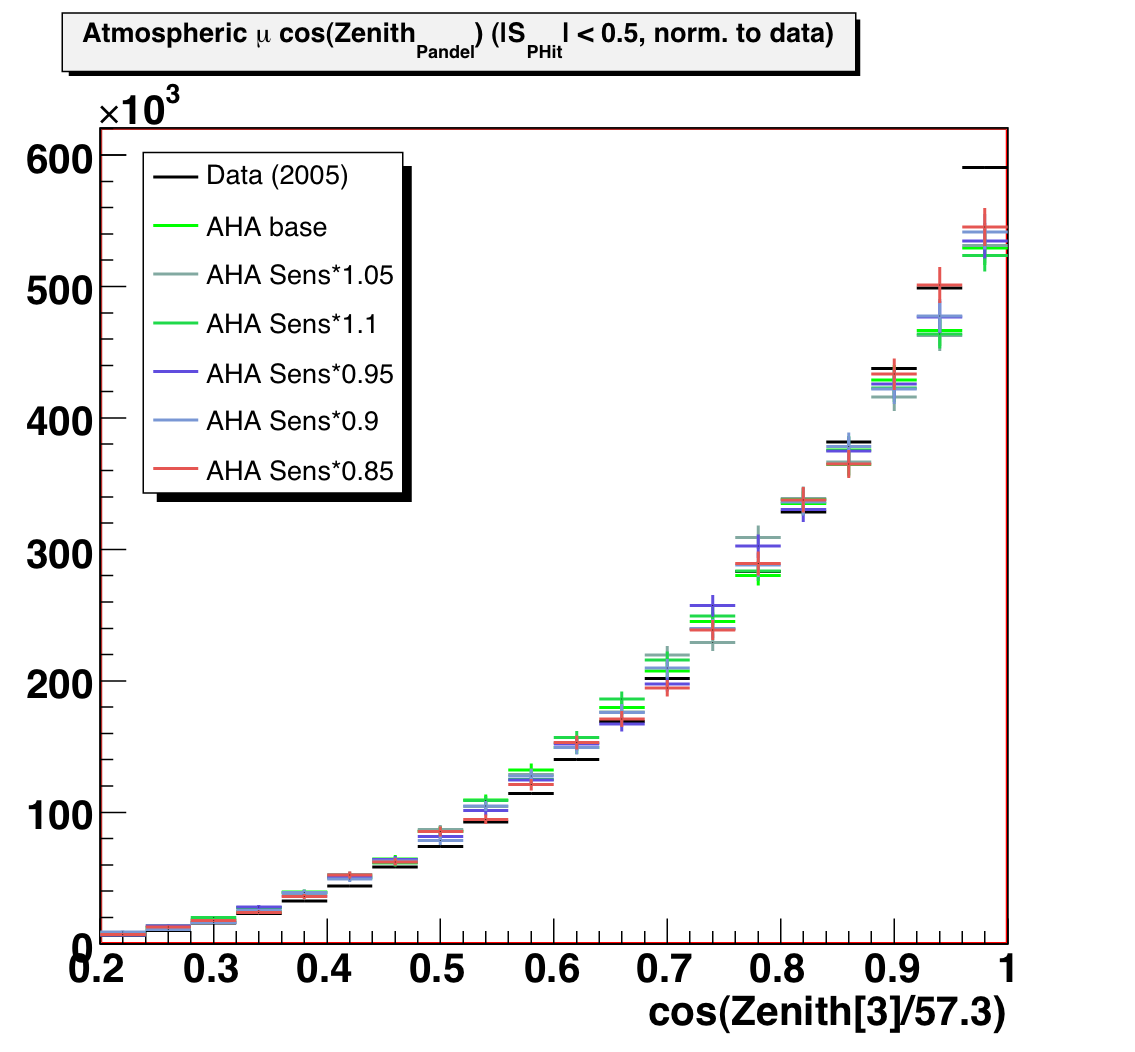
Figure 5: Downgoing muon reconstructed zenith angle, with a loose smoothness cut.
MC normalized to data for shape comparison.

I have also tried modifying the OM sensitivity and the PE distribution (JK PE with lower OM sensitivity). In this case, a 95% OM sensitivity is closest in normalization. The Nch plot does not seem to indicate a preference over this vs. old PE + 85% sensitivity, but I am continuing to investigate other variables.

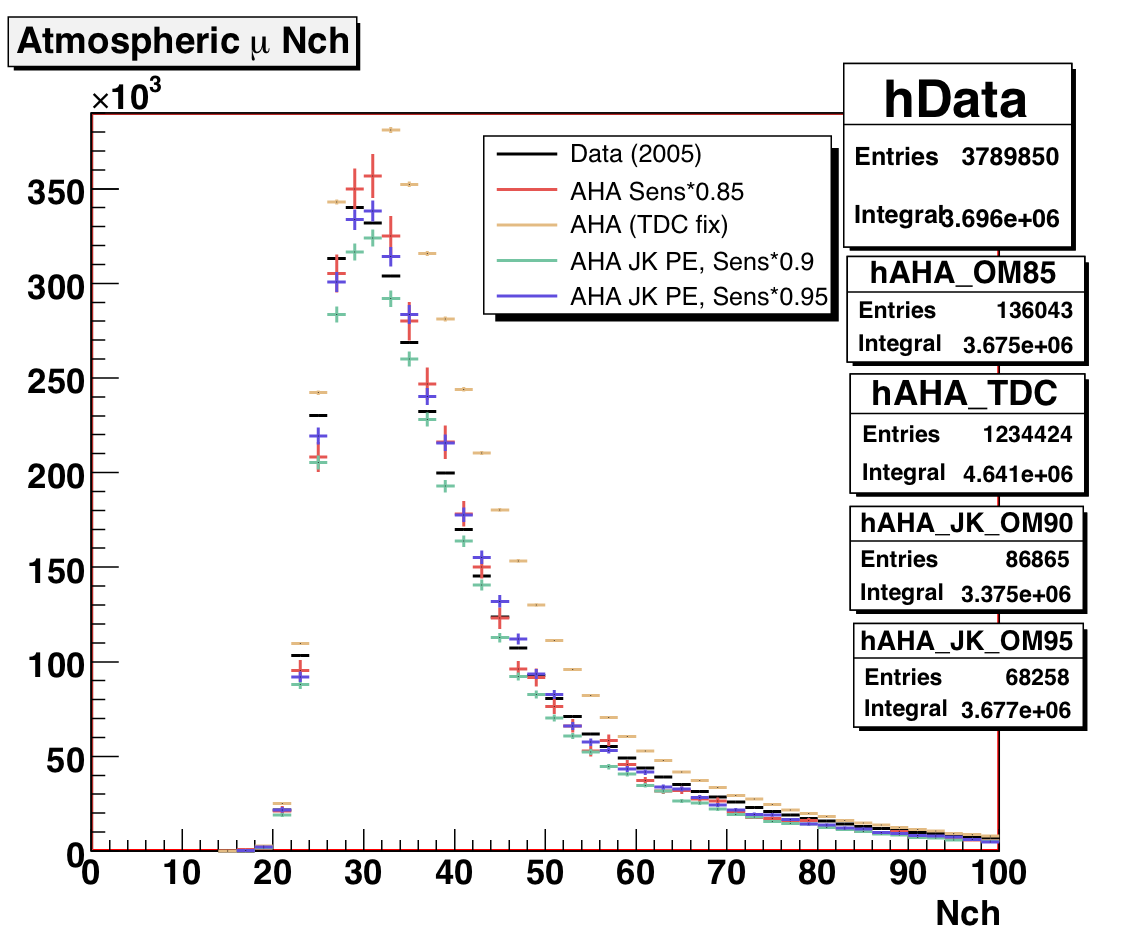
Figure 6: 2005 atmospheric muon MC at trigger level, Nch distribution for JK PE distribution and various OM sensitivities.

4. TDC and Trigger Time

The data/MC comparison of TDC indicated an offset in the trigger time in 2005 MC. This is possibly just a units confusion issue, as the correct trigger time for the Amasim steering file is found to be (0.96*10773 [old value] = 10342). 0.96 is the conversion from TDC channels to ns (or vice versa, I'm not sure).

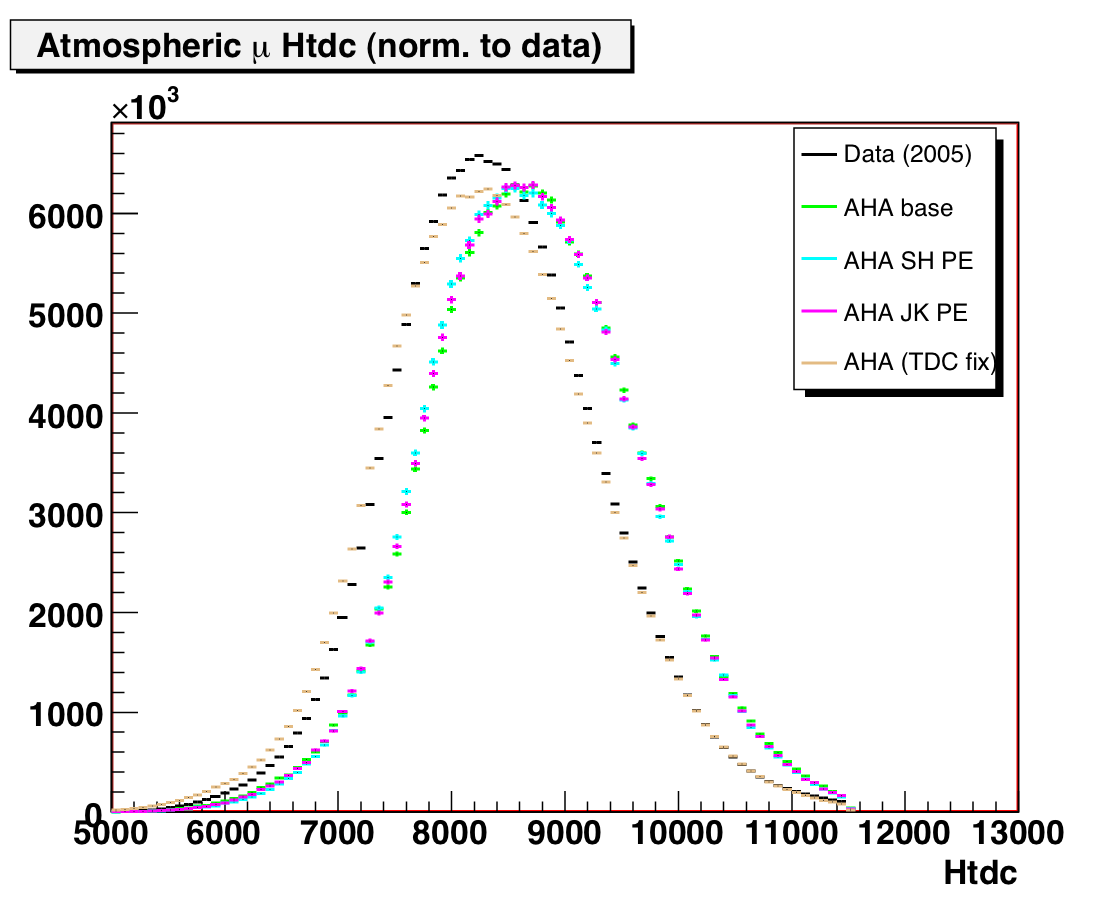
Figure 7: TDC for data/MC at trigger level. Corrected MC has a trigger time of 10342.