Possible Extensions¶
This section is going to be important in the future when we start testing real astrophysical models....Currently under Construction
Idea¶
One of the main disadvantages of the Simulations shown in the previous chapters is the lack of generality, which is due to the restrictions to one fixed mu per simulated Skymap. This obviously doesn’t comply with real source count distributions in our universe. In this Chapter the Analysis is therefore extended to Realistic Source Count Distributions. Although the origin of the Models are different, the basic idea for the sensitivity calculations is the same for all of them. Basically two conditions, or rather their corresponding integrals are evaluated:
The Sensitivity:
\(\Sigma_{exp}=\int_{0}^{\infty} \frac{d\Sigma_{0.1q}}{dN_{Sou}}\frac{dN}{d\mu} d\mu - \Sigma_{\mu=0}\) (for the 10% Quantile)
\(\Sigma=\int_{0}^{\infty} \frac{d\Sigma}{dN_{Sou}}\frac{dN}{d\mu} d\mu\) (for the Median)
And the conservations of the number of Signal Neutrinos:
\(n_{astro}=\int_{0}^{\infty} \frac{dN_{Sou}}{d\mu}\cdot\mu\cdot f(\gamma)d\mu\)
Here the parameter \(\Sigma_{exp}\) is the significance value taken from experimental data and \(\Sigma_{0.1q}\) is the Significance value of the test-statistics at the 10 percent quantile taken from pseudo exerpiments. The procedure can be interpreted as shifting the 10 percent quantile of the pseudoexperiments test-statistics on the experimental value, i.e., excluding a stronger signal with 90% C.L.
The variation of sources results in a significance shift, which can be parametrized with a simple powerlaw \(\frac{d\Sigma_{0.1q}}{dN_{Sou}}=a \cdot x^n\) as shown in the figure below for \(\gamma=2\)
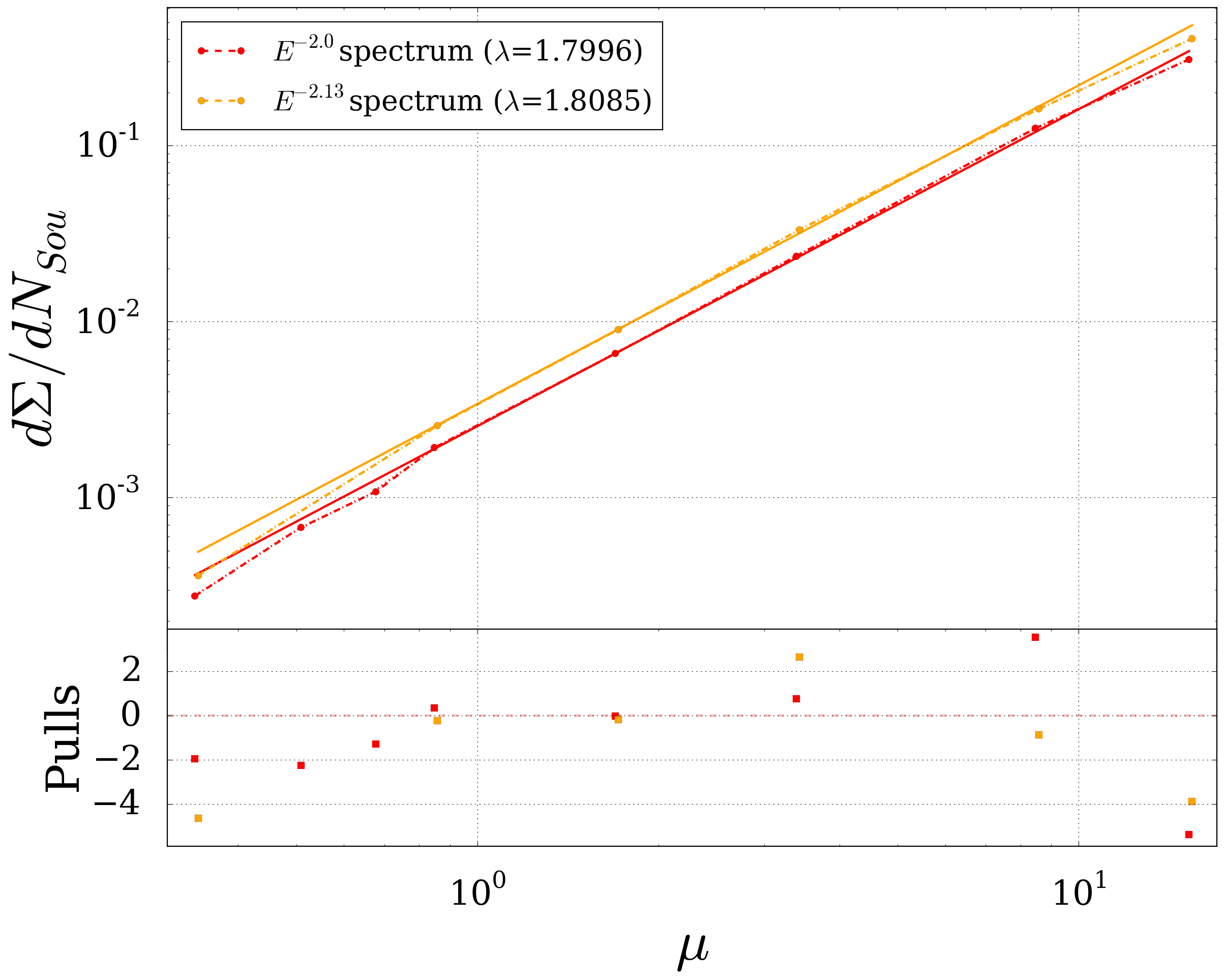
Fig. 40 Parametrisation of \(d\Sigma / dN_{Sou}\) for the 10% quantile as a function of \(\mu\). Best fit values for exponent \(\lambda\) are shown in the legend.
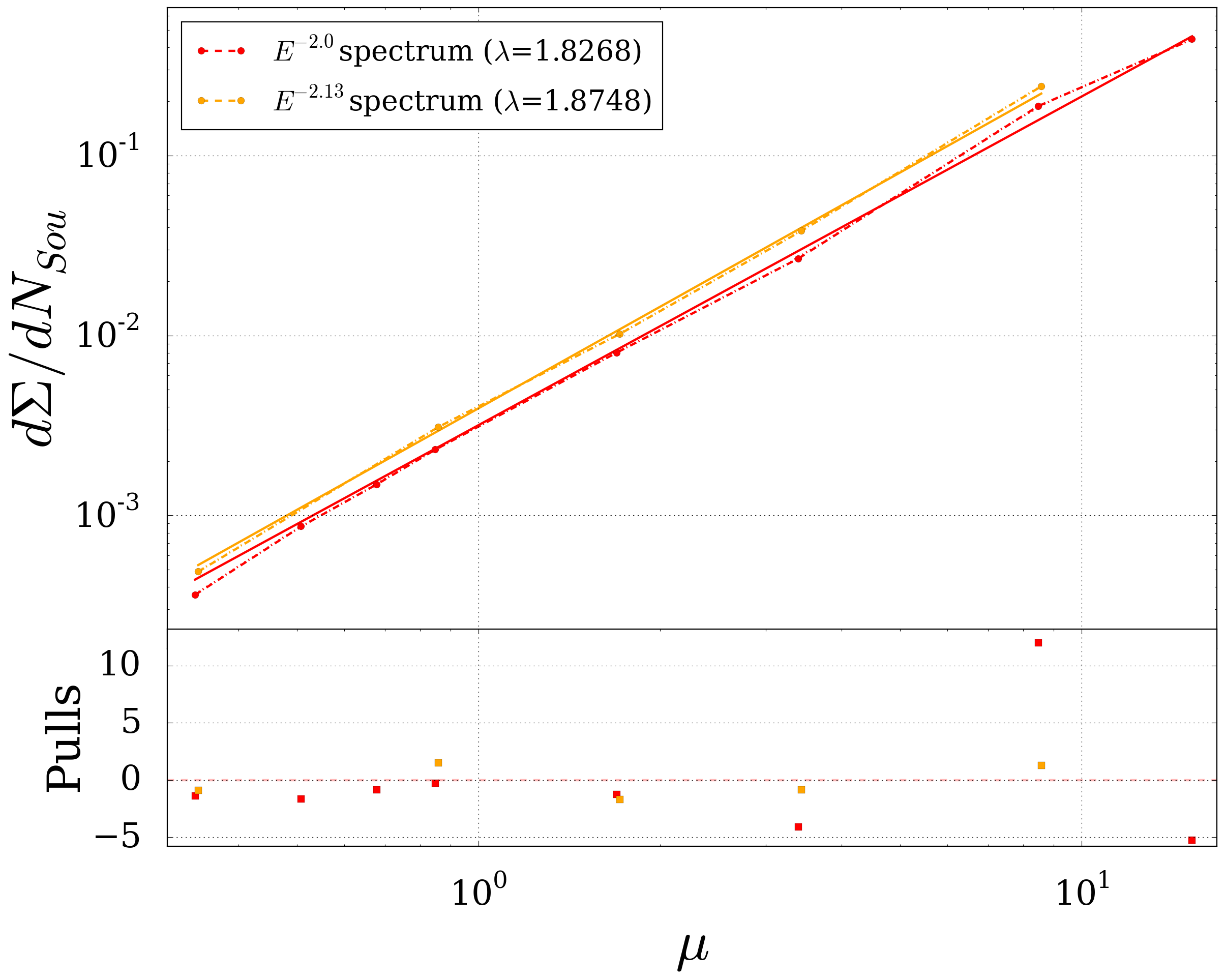
Fig. 41 Parametrisation of \(d\Sigma / dN_{Sou}\) for the median as a function of \(\mu\). Best fit values for exponent \(\lambda\) are shown in the legend.
It’s far from obvious that the integral above actually gives the correct value for the significance. In fact, having a look at the sensitvity plots reveals that the sensitivity doesn’t necessary grow linear in N. Consequently the functions \(d\Sigma / dN_{Sou}\) don’t follow a perfect power law. In order to show that the integral gives resonable results, a limited amount of skymaps with different mus is simulated. This procedure is very computational intesiv and is therefore only performed for a limited amount of skymaps and only for discrete mu values. One example of the significance distribution and the comparison to the integral method is shown below, others can be found here.
![_images/check_sigma[1707,426,106,47,17,4,1,1].png](_images/check_sigma[1707,426,106,47,17,4,1,1].png)
Fig. 42 Comparison of the significance of simulated multi-mu skymaps with the integral from above
Fermi-LAT Model¶
One possible scenario for the acceleration of cosmic rays is the so called hadronic model. This mainly implies that reactions in the acceleration are dominated by proton-proton collision
\(p+p \rightarrow K^{\pm}+\pi^{\pm}+....\)
and photonuclear interations
\(p+\gamma\rightarrow \Delta^+ \rightarrow p+ \pi^0 \rightarrow p+\gamma+\gamma\)
\(p+\gamma\rightarrow \Delta^+ \rightarrow n+ \pi^+ \rightarrow n+\mu^+ +\nu_{\mu}\)
where all the pions and kaons subsequently decay into neutrinos, leptons and photons. Assuming these mechanism to be present in cosmic ray sources, we expect a strong connection between the neutrino and the gamma ray flux.
Source Count Models from RLF¶
Assuming certain connections between the disc and the jet luminosity of AGNs, e.g. of FR-I and FR-II Radio Type Galaxies and Blazars, neutrino source count distributions can be interferred from Radio Measuerments [Willott et al(2001)][Dunlop et al (1990)].
Steep Source RLF¶
The group of steep spectrum sources consits mainly of sources of type FR-I and FR-II and have a characteristic spectral index \(\alpha_s\) of 0.8, equivalent to a particle spectrum \(p=2\alpha+1\approx 2.6\). The Radio Luminosity Function (RLF) is based on a sample of 356 sources selected by Willott et al[2000] and combines measurements from several radio catalouges at 178 MHz. Following it is possible to parametrize the RLF i.e. the number of sources per comoving volume and luminosity interval (\(\mathrm{d}N/(\mathrm{d}V \mathrm{d}\log_{10}(L))\)). As a simplification the function is described as the product of a luminosity dependent density \(\rho(L_{0.151})\) and a purely red-shift dependent and dimensionless evolution function f(z)
\(\rho(L_{0.151},z)=\rho(L_{0.151})\cdot f(z)\)
The dependence on red shift and luminosity is somewhat difficult and can only be parametrized by parts:
High Luminosity Sources:
\(\rho_h(L_{0.151})=\rho_h^0\cdot\left(\frac{L_{0.151}}{L_h^*}\right)^{-\alpha_h}\cdot \mathrm{exp}\left[L_h^*/L_{0.151}\right]\)
with evolution function:
Low Luminosity Sources:
\(\rho_h(L_{0.151})=\rho_l^0\cdot\left(\frac{L_{0.151}}{L_l^*}\right)^{-\alpha_h}\cdot \mathrm{exp}\left[L_{0.151}/L_l^*\right]\)
with evolution function:
The open parameters can be found in the paper written by Willott et al[2000]
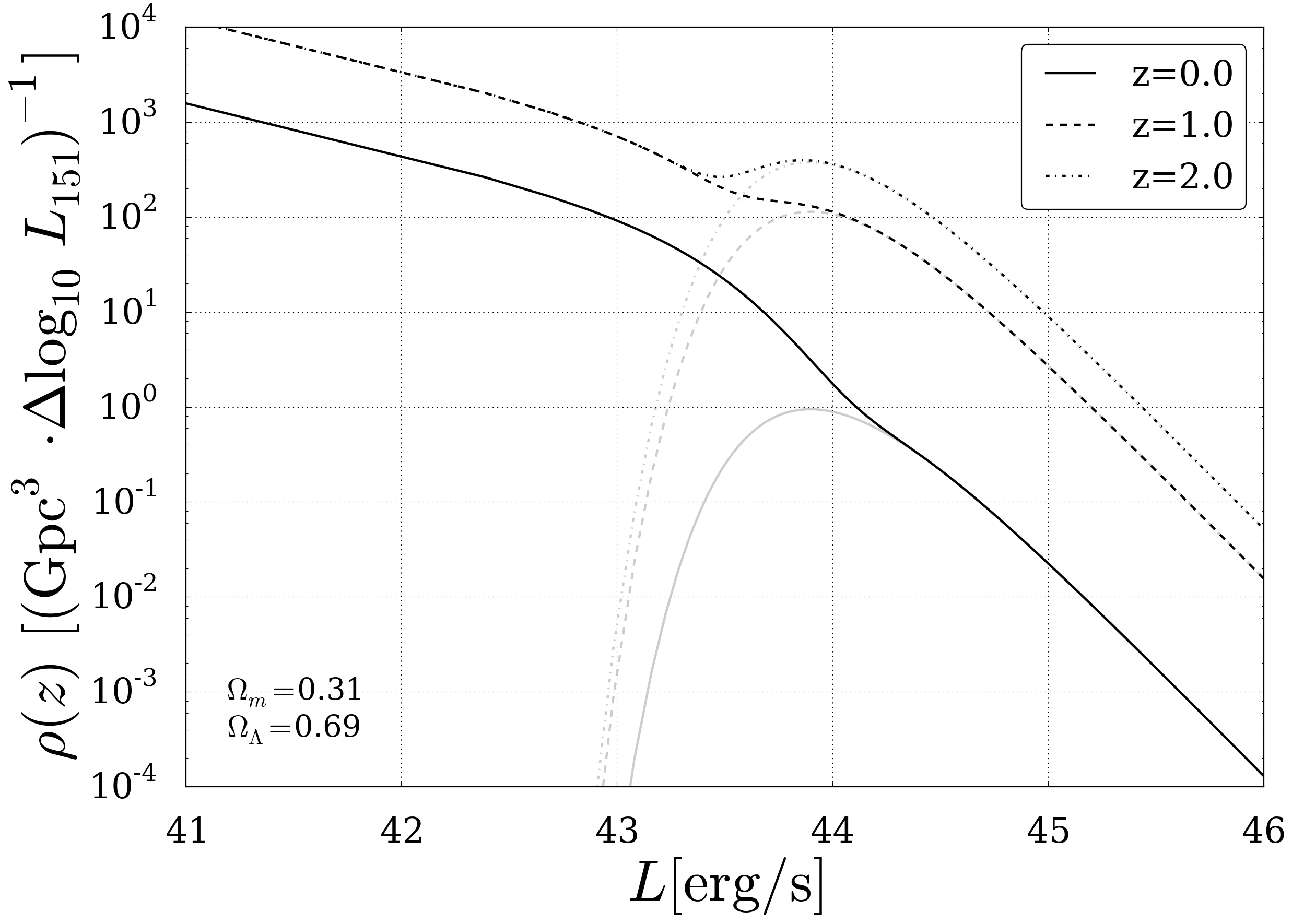
Fig. 43 The differential Radio Luminosity Function for Steep Spectrum Sources
Flat Source RLF¶
The catalouge by Dunlop et al [MNRAS (1990)] consists 171 flat sources, presumably mainly Blazars, measured at 2.7GHz with a spectral index of \(\alpha_f \approx 0\). For this group of AGN the RLF can be parametrized as
\(\rho(L,z)=\rho_0\cdot\left[\left(\frac{L}{L_c(z)}\right)^\alpha+\left(\frac{L}{L_c(z)}\right)^\beta \right]^{-1}\)
where the Luminosity-Redshift evolution is given by
\(\log_{10}(L_c(z))=a_0+a_1 \cdot z+a_2\cdot z^2\)
The parameters can be found in the corresponding paper resulting in the plot shown below.
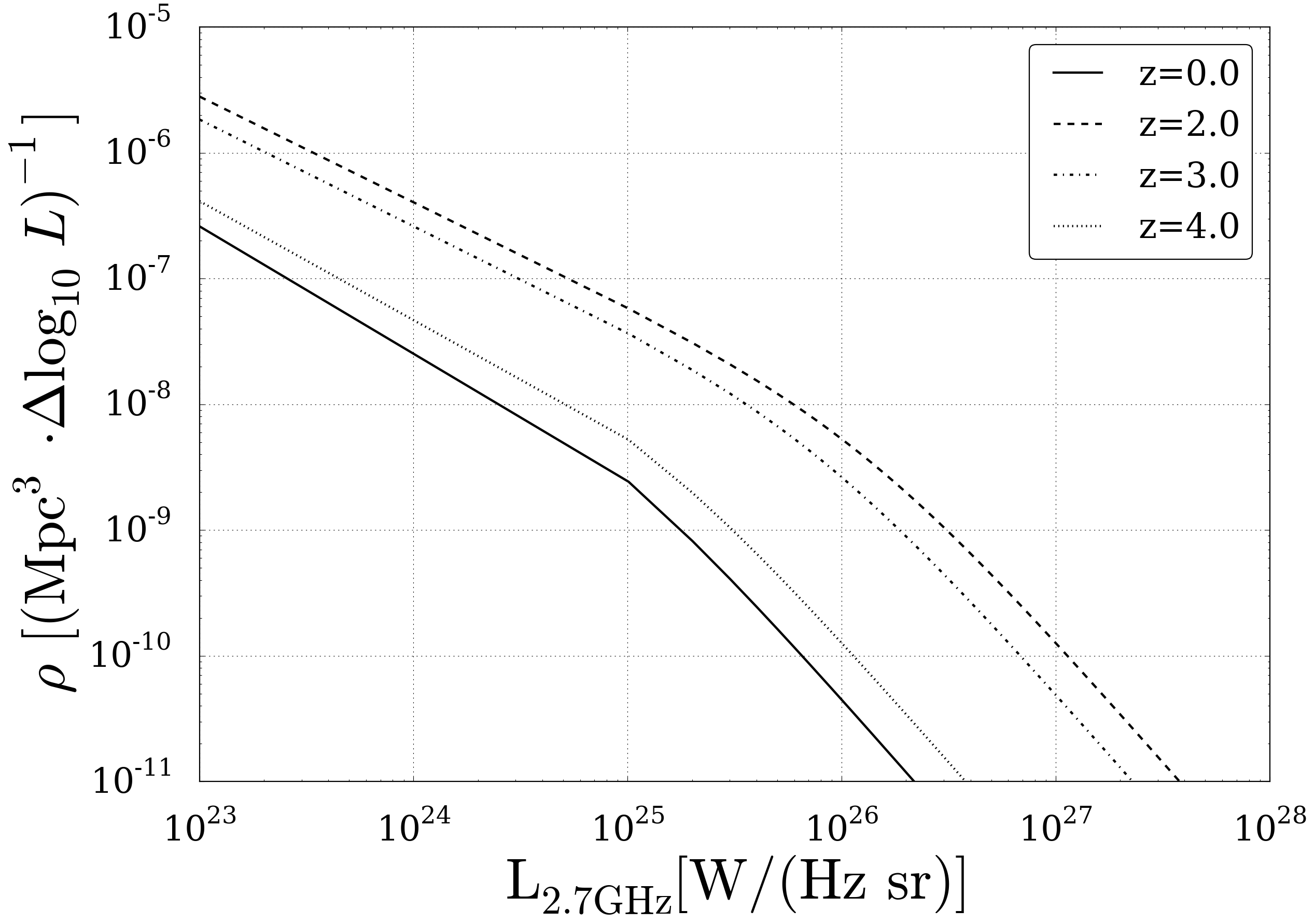
Fig. 44 The differential Radio Luminosity Function for Flat Spectrum Sources
Conversion into a Source Count Distribution¶
Assuming we have determined the Experimental Multipole Significance \(\Sigma_{exp}\) from our data we face the problem, that we can’t calculate the fraction of the flux that was actually clustered. The reason can be seen from the flux plots in section Performance , where the flux sensitivity apparently doesn’t fall with \(1/N_{Sou}\). Hence the fraction of the clustered flux for the same sensitvity is smaller when only a small number of sources contributes.
In order to test the RLFs from above the density functions (\(\mathrm{d}N/(\mathrm{d}V \mathrm{d}\log_{10}(L))\)) have to be converted to Source Count Distributions (\(\mathrm{d}N/\mathrm{d}\mu\)). The most important equation here is the relation between the luminosity and the source strength parameters \(\mu\)
\(\mu=\frac{L}{4\pi\cdot d_L}\cdot b(\gamma)\)
with the redshift-dependent luminosity distance and a the conversion factor \(b(\gamma,z)\)
\(b(\gamma,z)=\frac{\sum T_x \cdot \int_0^{\infty}A_{eff}(E)\cdot E^{-\gamma}\mathrm{d}E}{\int_0^{\infty} E^{1-\gamma}\mathrm{d}E}\)
In order to derive this expression we make use of the fact that we can express the total energy by integrating over the neutrino flux
\(E_{ges}=\int_0^{\infty} E \cdot \Phi_0 \cdot E^{-\gamma}\mathrm{d}E\)
In case the flux from the source \(\frac{L}{4\pi\cdot d_L}\) is equivalent to \(E_{Ges}\) we know from the diffuse fit that we have \(n_{sig}\) corresponding signal neutrinos. Since we assume the neutrino flux to assume the same powerlaw for all sources we can therefore conclude that only the flux normalisation changes and hence \(\mu \propto L\). This lead to the expression
\(\frac{\mu\cdot E_{Ges}}{n_{sig}}=\frac{L}{4\pi\cdot d_L}\)
plugging in the expression for \(E_{Ges}\) and the exposure gives the final expression
\(\mu\cdot\frac{1}{b}=\mu\cdot\frac{\int_0^{\infty}(E)^{1-\gamma}\mathrm{d}E}{\sum T_x \cdot \int_0^{\infty}A_{eff}(E)\cdot (E)^{-\gamma}\mathrm{d}E}=\frac{L}{4\pi\cdot d_L}\)
where the flux normalisation has already been canceled out.
Now the RLF is simultaneously integrated and converted to source count parameters, i.e. the number of sources dN for fixed L,z (with corresponding \(\mu\)) is calculated as \(\rho(L,z)\cdot(dV/dz)\cdot dz dL\) and saved in a histogram with N as function of \(\mu\). The Luminosity given in these equations is the total Luminosity of the astrophysical object, which can be calculated from the differential Luminosity \(L_{m}\) measured with the Radio telescopes at a fixed frequency \(\nu_m\) assuming the given spectral index \(\alpha_x\) and hence
\(L_{tot}=\int_{0}^{5GHz} L_{m}\cdot \left(\frac{\nu}{\nu_m [GHz]}\right)^{-\alpha_x} \mathrm{d}\nu\)
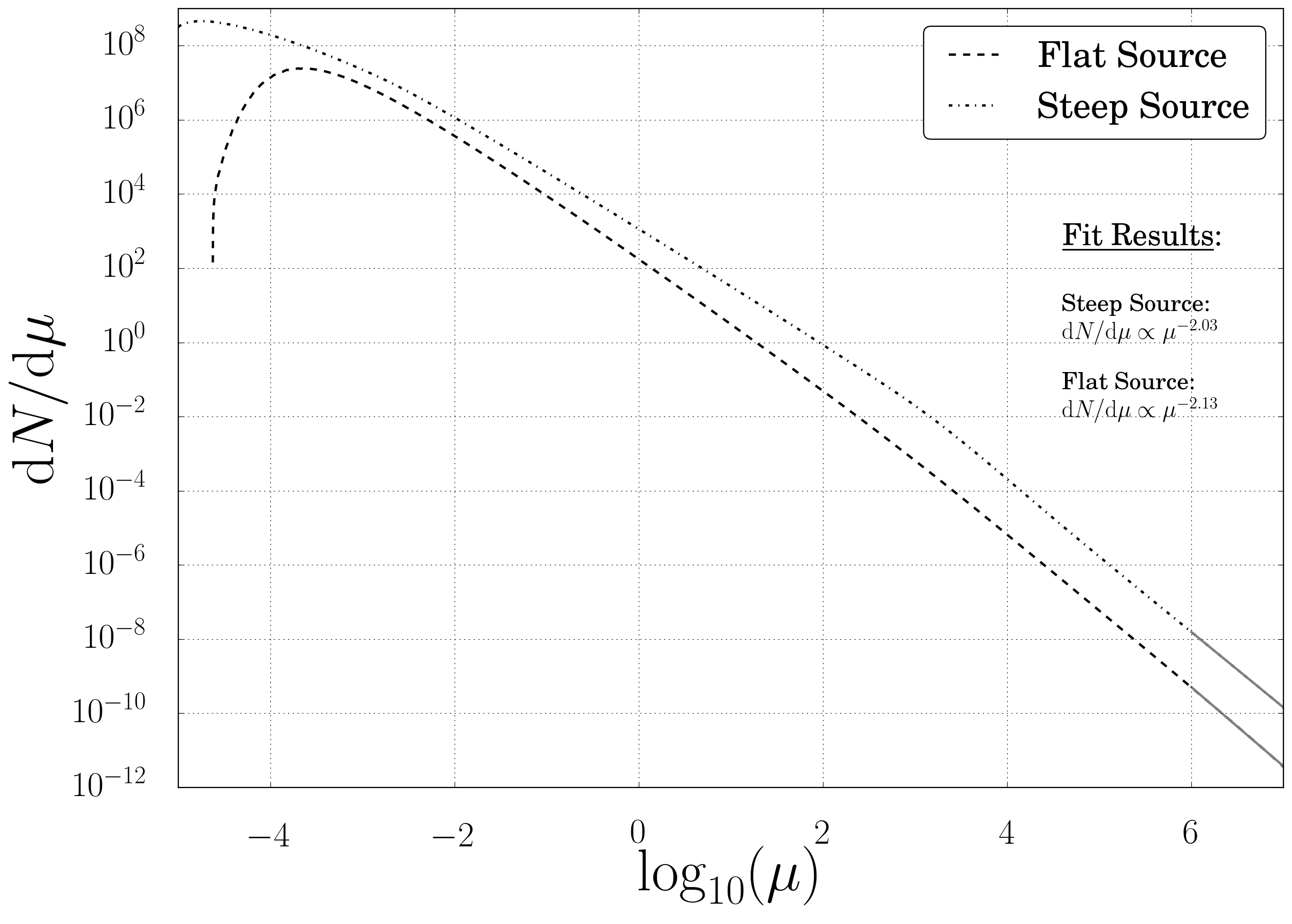
Fig. 45 Resulting Source Count Distribution for both source types
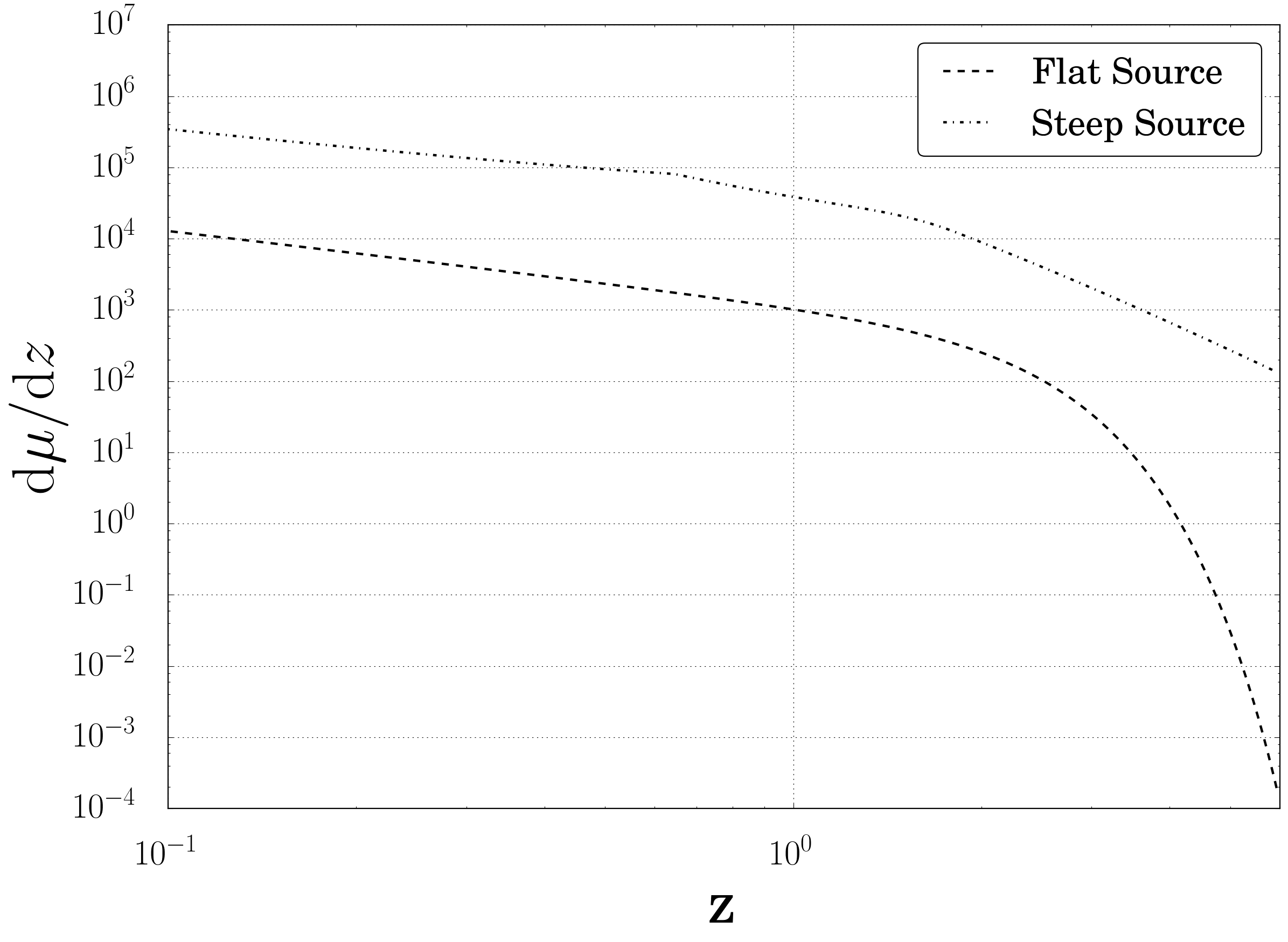
Fig. 46 Contribution to the total flux from different z values
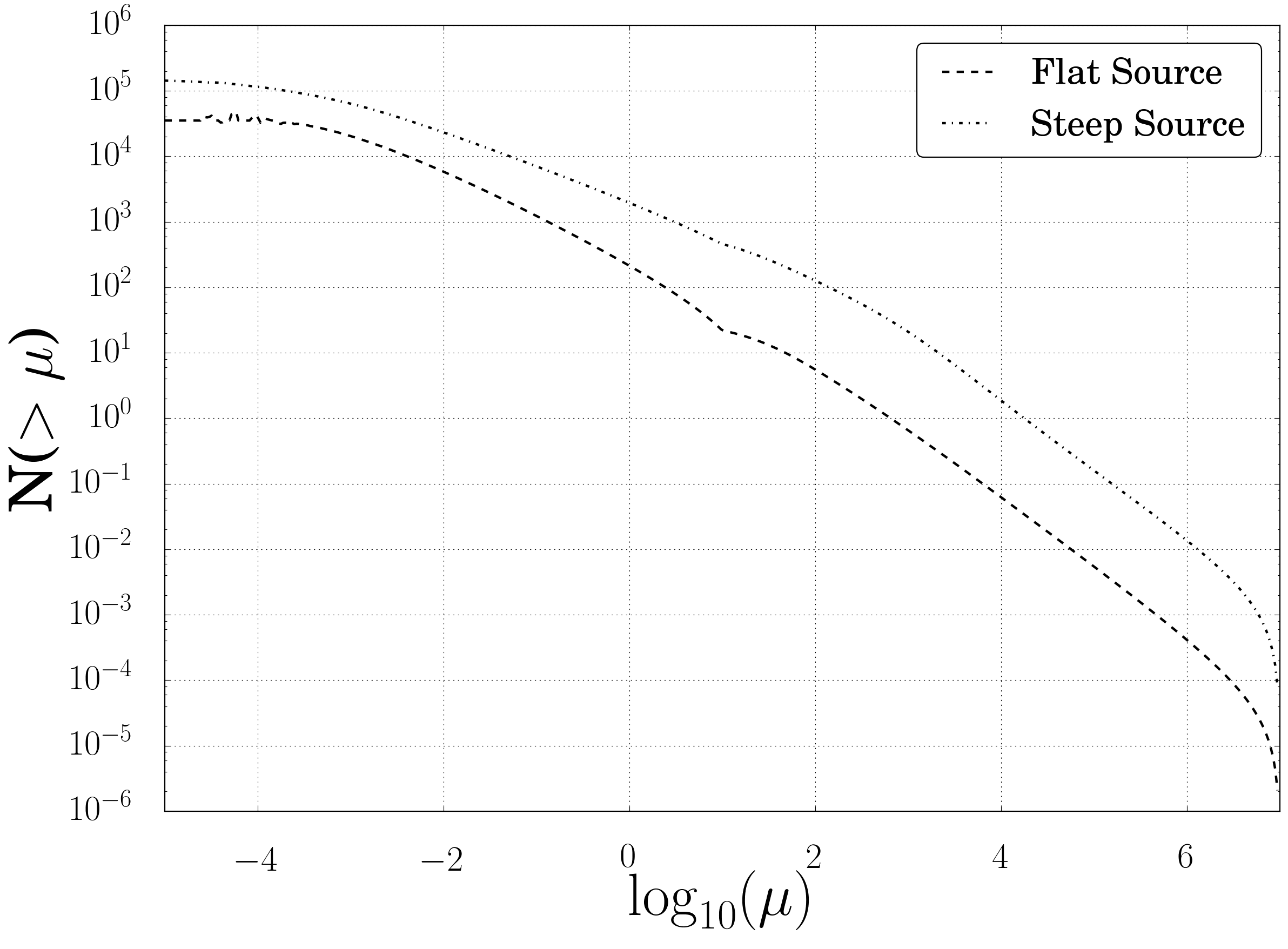
Fig. 47 Number of Sources stronger then \(\mu\)
Cross Correlations with the NVSS Sky Survey¶
The NRAO VLA Sky Survey (NVSS) is a radio survey containing almost 2 million distinct sources measured with the Very Large Array (VLT) at a frequenzy of 1.4 GHz and a declination of \(\delta>-40^{\circ}\) (see skymap visualization in galactic coordinates below). In the case that the observed cosmic neutrino flux has its origin in these type of sources there should be significant cross-corellations between the sources positions in the survey and the one that IceCube measures. Since the Multipole-Analysis is carried out in the parameter space of spherical harmonics cross-correlations can be included by modifying the power spectrum
where the \(a_l^m\)‘s and \(b_l^m\)‘s represent the neutrino skymaps and the NVSS skymaps expansion coefficients, respectively. Using the transformed power spectrum the test statistic can be calculated as before. The plot below shows the shift in the test statistic that results from letting the simulated neutrino position coincide with the 10 strongest sources from the survey in comparison to 10 randomly chosen source positions.
Fig. 48 The energy flux from the Radio Sources in the NVSS Survey shown in galactic coordinates.
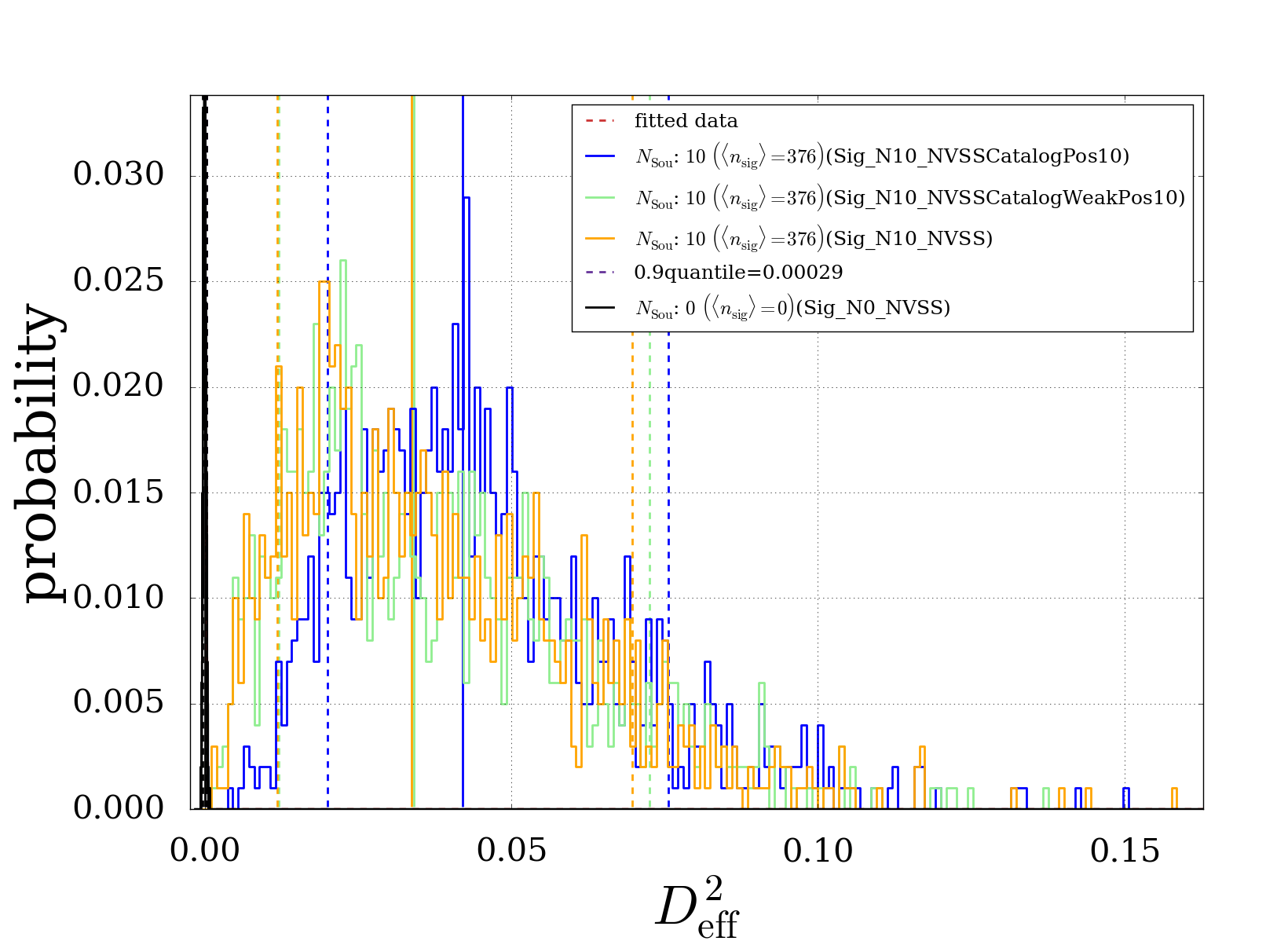
Fig. 49 The Test-Statistic shift resulting from cross corellation simulations